Solving Matrices using Microsoft Excel
A trunnion of diameter 12.363” has to be cooled from a room temperature of 800F before it is shrink fitted into a steel hub. The equation that gives the diametric contraction ΔD of the trunnion in a dry-ice/alcohol mixture (boiling temperature is -1080F) is given by:
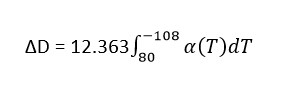
The equation for the thermal expansion coefficient, α= α1 + α2T+ α3T2, is obtained using regression analysis where the constants of the model are found by solving the following simultaneous linear equations.

Find the values of a1, a2 and a3
Watch Solution on YouTube: https://www.youtube.com/watch?v=o1SpDASt1nw
If you like this video, please click on the Subscribe button for more standard tutorial videos »
Regression with Excel
A 20L storage tank is filled with ammonia (NH3) and the storage has an over-design factor (pressure design factor) of 10% and the bursting pressure rating (Pmax) of 3500psi. The Redlich-Kwong (RK) equation of state can be used to evaluate the pressure as a function of temperature, T(K) and molar volume, V (m3/mol) and the mathematical expression of RK equation is shown by:
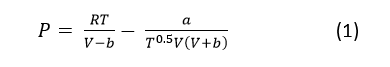
Where P is the pressure (Pa), R is the universal gas constant (8.3145 J/mol K), T is the temperature (K), V is the molar volume (m3/mol), and
are the RK equation constants which can be calculated using Eq. (2) and (3) respectively:
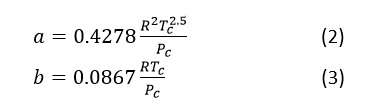
Where is the critical temperature for NH3 gas (405.5K) and
is the critical pressure for Cl2 gas (1636 psi)
Prepare a spreadsheet using Microsoft Excel to solve the following cases:
- If the tank is charged with 5kg ammonia, what is the maximum safe operating temperature (Tsafe) for this storage tank?
- At 4800C, what is the maximum mass of ammonia that the storage tank can hold safely? Hint: Pick an initial guess on mass of ammonia between 2kg and 7kg
- What are the potential safety risks associated with the use of this tank system at 1000C. Evaluate the vapour pressure using Antoine equation and comment on your finding.
Log10(P*) = = A – (B/(C+T))
Where P* is saturated pressure (bar), A, B and C are the Antoine coefficient in which the numerical values for pure ammonia are A = 4.86886, B = 113.928 and C = -10.409
Other Information:
1 bar = 100,000 J/m3; 1 bar = 14.5038 psi; 00C = 273.15 K; Molecular weight of NH3 = 17.03 g/mol
Pmax = 1.1 Psafe
Watch Solution on YouTube: https://www.youtube.com/watch?v=nzhjETKdpn0
If you like this video, please click on the Subscribe button for more standard tutorial videos »
Friction Factor Calculation on Excel (Iterative calculations)
Chemical, Civil and Mechanical Engineers must often determine the power required to pump a fluid through a series of pipes. To dod so, we must first determine a friction factor. If the fluid flow is turbulent, (Re > 2300) and the pipes are smooth, the friction factor can be determined as:
f=0.0396Re-0.2
In this equation, f represents the friction factor, appositive value that does not exceed 0.1, and the Re represents the Reynolds (Re) number, which is a function of the fluid properties, the pie diameter and the nominal fluid velocity.
For laminar flow regime (Re ≤ 2300), the friction factor may be determind as:
f= 8/Re
The Re increases with increasing fluid velocity and may be determined as
Re= ρUd/μ
Where ƿ is the density of the fluid, U is the fluid velocity, d is the pipe diameter and µ is the fluid viscosity.
Reference data:
Fluid density at 250C, ρ=789 kg/m3
Fluid viscosity at 250C, μ=1.2318 x 10-3 Pa.s
Diameter of circular pipe = 5 mm
Formula: Fluid Velocity,
U= (Volumetric flow rate (m3/s))/(Cross-sectional area of circular pipe (m2))
- Using Excel, calculate the values and fill u the following tables with reference to the given formulae and data.
- Plot a graph of pressure drop (kPa) against volumetric flow rate (mL/s or m3/s) with the results in (a) using Excel. Assuming the relationship between the pressure drop and volumetric flow rate is linear, develop an empirical equation using Microsoft Excel Regression Tool.
- Based on the model developed by Larman-Prandtl, if the fluid flow is turbulent (Re > 4000) and the pipes are smooth, the friction factor can be determined as:
1/√f = 1.930log10 (Re√f)-0.537
Using iterative methods (e.g goal seeker or solver), determine the values of the friction factor corresponding to Reynolds numbers of 5000, 10000, 15000, 20000 and 25000. (Leave all solutions in 4 significant figures)
| Pressure Difference (kPa) | Volumetric flow rate (mL/s) | Fluid Velocity (m/s) | Reynolds number | Friction factor |
| 0.62 | 3.87 | |||
| 0.94 | 4.49 | |||
| 1.13 | 5.26 | |||
| 1.72 | 5.43 | |||
| 2.34 | 6.02 | |||
| 2.70 | 6.44 | |||
| 2.98 | 6.87 | |||
| 4.05 | 7.55 | |||
| 4.54 | 7.73 | |||
| 5.32 | 8.42 | |||
| 5.98 | 8.75 | |||
| 6.12 | 10.32 | |||
| 6.73 | 10.79 | |||
| 7.78 | 11.32 | |||
| 10.00 | 14.13 |
Watch Solution on YouTube: https://www.youtube.com/watch?v=vXC7FzugNFA
If you like this video, please click on the Subscribe button for more standard tutorial videos »
