- a) Use Gauss – Jordan Row – Operation technique to determine the values of p, q and r that would satisfy the following system of linear equations:
p+q +r + 3 = 0
2p-3q+2r-9=0
4p+q-3r-11=0
- b) Use Matrix Inverse method to solve for, m1, m2 and m3 that satisfy each of the equations.
Round up the values of the unknowns obtained to the nearest whole number.
25m1+25m2+25m3 = -75
22m1-33m2+22m3= 99
24m1+6m2-18m3 =66

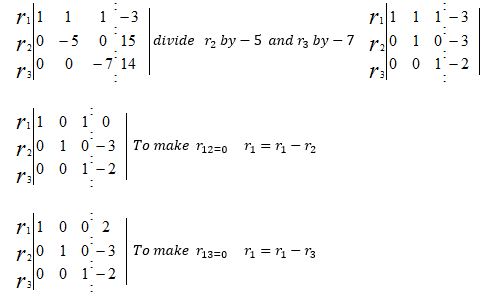
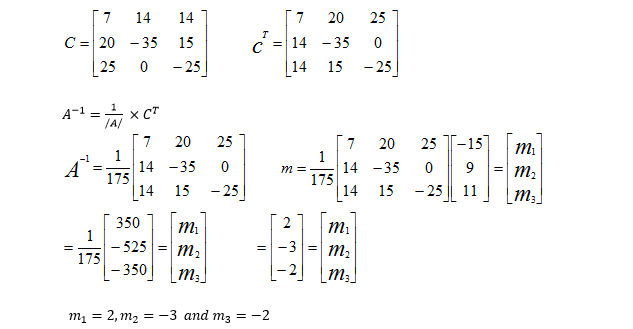
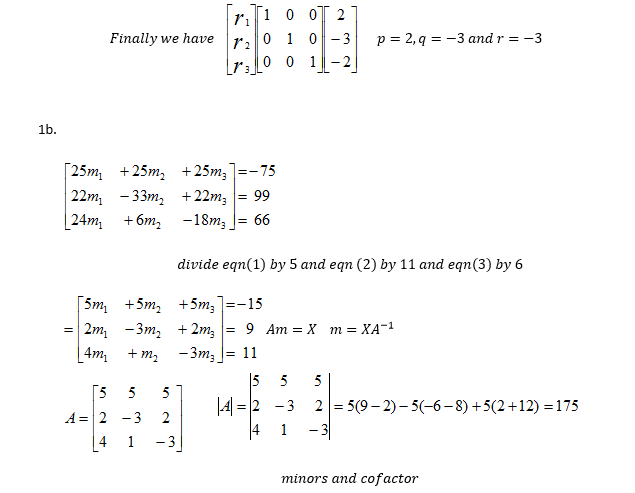
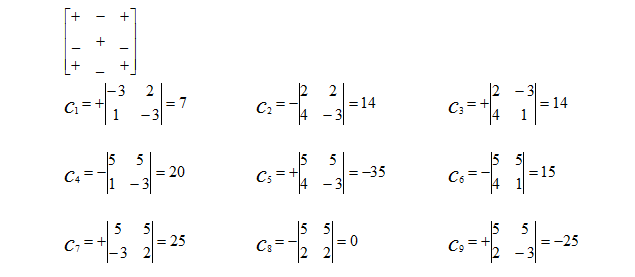
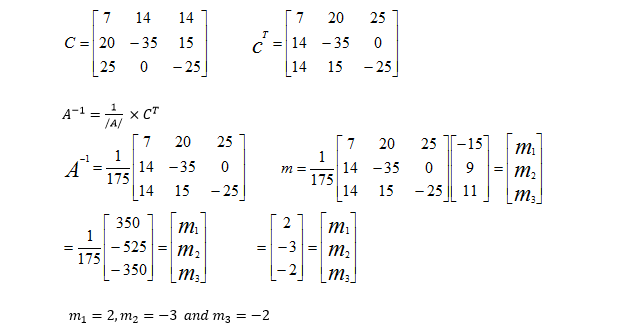
2
a. A plastic sphere having a specific gravity and diameter of 0.65 and 0.11 m respectively, is thrown into a water reservoir for 50 experimental trials. In each of the trick the partial submerged depth (x) of the sphere is measured and recorded. Subsequently, an equation was derived based on the measured submerged depths and one other variable influencing the depth of submergence. The equation was developed to allow for prediction of the sphere’s submerged depth. The resulting equation from the process is given as in Eq. Q2
y = f(x) = x3 – 16.5 x 10-2 x2+ 39.93 x 10-5 = 0
State the values of the submerged depths when the sphere floats completely on the water surface and when it fully submerged, respectively. Use these values as the boundary conditions over which the partial submerged depth of the sphere lies which represents the root solution) of the derived equation
b. What is the ratio of the sphere’s submerged to exposed diameter in this typical case? What do you think is responsible for the sphere’s partial submergence?
Q2a)
R.D = 0.65 d = 0.11m
F(x) = x3 – 16.5 x 10-2 x2 + 39.93 x 10-5 = x3 – 0.165 x2 + 0.0003993
When the sphere float x = 0
When the sphere is fully submerged x = 0.11m
a = 0 , b = 0.11 our boundary condition
false position method, 8 iteration
xe = [af(b) – bf(a)]/ f(b) – f(a)
n = 0, a = 0, b = 0.11
f(a) = f(0) = 2.662 x 10-4
| n | a | b | f(a) | f(b) | Xe | f(Xe) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0.11 | 39.93 x 10^-5 | -2.66 x 10^-4 | 0.066 | -ve |
| 1 | 0 | 0.066 | 39.93 x 10^-5 | -3.194 x 10^-5 | 0.0611 | +ve |
| 2 | 0.0611 | 0.066 | 1.1419 x 10^-5 | -3.194 x 10^-5 | 0.06239 | -ve |
| 3 | 0.0611 | 0.06239 | 1.1419 x 10^-5 | -1.106 x 10^-7 | 0.062378 | -ve |
| 4 | 0.0611 | 0.062378 | 1.1419 x 10^-5 | -3.5356 x 10^-9 | 0.062378 | -ve |
| 5 | 0.0611 | 0.0623776 | 1.1419 x 10^-5 | -1.647 x 10^-10 | 0.062378 | -ve |
| 6 | 0.0611 | 0.0623776 | 1.1419 x 10^-5 | -1.647 x 10^-10 | 0.062378 | -ve |
| 7 | 0.0611 | 0.0623776 | 1.1419 x 10^-5 | -1.647 x 10^-10 | 0.062378 | -ve |
| 8 | 0.0611 | 0.0623776 | 1.1419 x 10^-5 | -1.647 x 10^-10 | 0.062378 | -ve |
x = 0.062776m
2b)
submerge depth = 0.06378
exposed diameter = 0.11 – 0.06278 = 0.4722
ratio = 0.06278/0.04722 = 1.329
The specific gravity of the sphere is less than 1 hence its partial submergence
a) Use the Predictor Corrector method to solve the equation: 𝜕𝑦/𝜕𝑥=2𝑥−𝑦 ,
for x=0(0.2)0.4
given that x= 0 when y1=1.
b) Use the Euler’s method to solve the equation above and determine which method is more accurate if the exact solution is: 𝑦=2𝑥−2+3/𝑒𝑥
3a) Predictor Corrector
dy/dx = 2x – y x = 0(0.2)0.4 y(0)= 1
xo = 0, x1 = 0.2 x2 =0.4 h=0.2
𝑦1̅̅̅= 𝑦𝑜+ℎ𝑓(𝑥𝑜,𝑦𝑜) =1+0.2(2(0)−1)=0.8
y1=𝑦𝑜+ℎ/2(𝑓(𝑥𝑜,𝑦𝑜)+𝑓(𝑥1,𝑦1̅̅̅ ) ) = 1+0.2/2[(2(0)−1)+2(0.2)−0.8]=1.7
𝑦2̅̅̅=𝑦1+ℎ/2(3𝑓(𝑥1,𝑦1)−𝑓(𝑥2,𝑦0 ) )=1.17+0.2/2[(3(2(0.2)−1.17)+2(0.4)−1)]=0.959
𝑦2=𝑦1+ℎ/2(𝑓(𝑥1,𝑦1)−𝑓(𝑥1,𝑦1̅̅̅ ) )=1+0.2/2[(2(0.2)−1.17)+2(0.4)−0.959)]=1.0771
n | Xn | Yn | ~Yn |
0 | 0 | 1 | – |
1 | 0.2 | 1.17 | 0.8 |
2 | 0.4 | 1.0771 | 1.17 |
3b) Euler
n | Xn | Yn | ~Yn |
0 | 0 | 1 | -1 |
1 | 0.2 | 0.8 | -0.4 |
2 | 0.4 | 0.72 |
|
Y’ = dy/dx = 2x –y
Y’0 = 2(0) – 1 = -1
n=1
y1 =y0 + hy’0 = 1 + 0.2(-1) =0.8
y’1 = 2x1 – y1 =2(0.2) -0.8 =0.4
n=2
y2 =y1 + hy’1 =0.8 + 0.2(-0.4) =0.88
Exact solution is y = 2x – 2 + 2/e3
a. Find the Eigen values and their corresponding Eigen vectors of the matrix.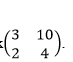
b. Use the Eigen values and Eigen vectors calculated above to determine the solution (f1(x) and f2(x)) of the system of ordinary differential equations below:
f’1 (x) =3 f1 (x) + 10f2 (x)
f’2 (x) =2 f1 (x) + 4f2 (x)
Given that f1(0)= 0; f2(0) =1
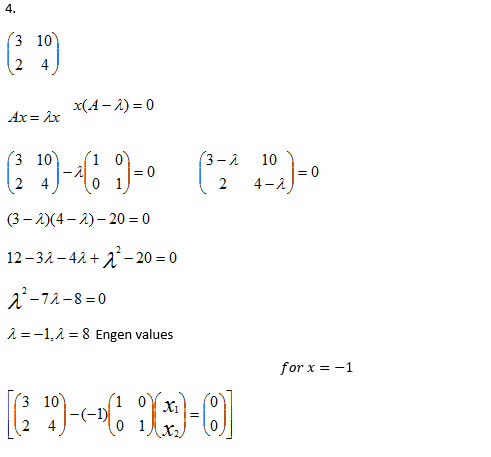
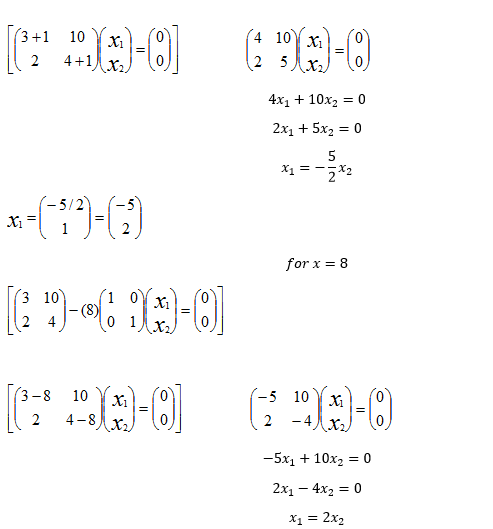
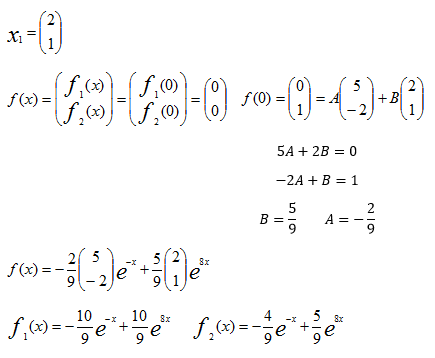
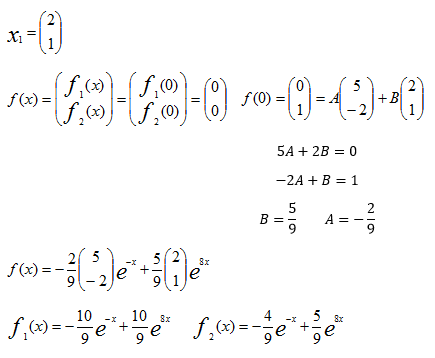
F1 (x) -30/9 e-x + 10/9 e8x F2 (x) -4/9 e-x + 5/9 e8x
F’1 (x) = -30/9 e-x + 30/9 e8x – 40/9 e-x + 40/9 e8x
F’2 (x) = 16/9 e-x + 20/9 e8x – 16/9 e-x + 20/9 e8x
a. Use forward, backward and central difference approximations, respectively. To estimate the first derivative of f(x)= x3+3x2+2x+1 at x= 0.75 and h= 0.25.
b. Apply Simpson’s rule to evaluate x+1dx using 8 intervals correct to 4 decimal places.
5a)
𝑓(𝑥)=𝑥3+3𝑥2+2𝑥+1,
𝑥=0.75, ℎ=0.25.
Backward difference,
𝑌′= (𝑌𝐼−𝑌𝐼−1 )/ℎ,
Forward difference
𝑌′=(𝑌𝐼+1− 𝑌𝐼 )/ℎ
central difference
𝑌′=(𝑌𝐼+1−𝑌𝐼−1 )/2ℎ
𝑦𝑖= 𝑦(𝑥) =0.753 + 3(0.75)2 + 2(0.75) + 1=4.609375
𝑦𝑖+1 = 𝑦(𝑥+ℎ) = 𝑦(1) =13 + 3(1)2 + 2(1) + 1 = 7
𝑦𝑖−1= 𝑦(𝑥−ℎ) = 𝑦(0.5) = 0.53 + 3(0.5)2 + 2(0.5) +1 = 2.875
Therefore;
Backward, 𝑦′=6.9375.
Forward, 𝑦′=9.5625.
Central 𝑦′=8.25
5b)
∫02(𝑥+1)2𝜕𝑥
𝑛=8,
𝑑=(𝑏−𝑎)/𝑛 =(2−0)/8=0.25.
𝑦=(𝑥−1)2
| x | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 |
|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1.5625 | 2.25 | 3.0625 | 4 | 5.0625 | 6.25 | 7.5625 | 9 |
𝐼 = 𝑑/3[(𝑦1+𝑦9)+2(𝑦3+𝑦5+𝑦7)+4(𝑦2+𝑦4+𝑦6+𝑦8)]
𝐼 = 0.25/3[(1+9)+ 2(2.25+4+6.25)+ 4(1.5625+3.0625+5.0625+7.5625)]
𝐼=8.5
a. What are the key constraints common to all linear programming problems?
b. Use graphical solution to maximize y + x = M subject to the following constraints:
𝑥≥1; 𝑦≥0; 𝑦≤𝑥; 𝑦≤2 𝑎𝑛𝑑 𝑥≤3
6a)
𝑥=0 & 𝑦=0
6b) 𝑥≥1, 𝑦≥0, 𝑦≤𝑥, 𝑦≤2, 𝑥≤3.
There are corners at (1,0), (3,0), (3,2), (2,2), and (1,1).
Y + x = m
S/N | (x,y) | M |
1 | (10) | 1 |
2 | (3,0) | 3 |
3 | (3,2) | 5 |
4 | (2,2) | 4 |
5 | (1,1) | 2 |
M Is maximum at 5 when x=3 and y=2.
7a. Consider the nonlinear equation ex– x – 2 = 0
i. State the intermediate value theorem (IVT)
ii. Show there is a root a in the interval (1,1.5). Hint: Use the IVT
b.
i. Estimate how many iterations will be needed to approximate this root with an accuracy of e= 0.01 using the bisection method.
ii. Approximate with an accuracy of E=0.01 using the bisection method.
7a)
- If f is a continuous function whose domain is the interval [a, b], then it takes in any value between f (a) and f (b) at some point within the interval.
- 𝑓(𝑥)=𝑒𝑥−𝑥−2
At x = 1.0 𝑓(𝑥)=𝑒1−1−2 = −0.2817
At x = 1.5 𝑓(𝑥)=𝑒1.5−1.5−2 = 0.9819
Therefore at x = 1, the curve is below zero
At x = 1.5, the curve is above zero.
Hence there is a root of the polynomial in the interval.
6b) No of iterations
𝑛≥ [ln(𝑏−𝑎)−ln𝜀] /ln2
= [ln(1.5−1)−ln0.01]/ ln2= 5.6 ≈ 6
| n | a | b | c | F(c) | b.c | f(a).f(c) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1.5 | 1.25 | 0.240343 | 0.25 | – |
| 2 | 1 | 1.25 | 1.125 | -0.04478 | 0.125 | + |
| 3 | 1.125 | 1.25 | 1.1875 | 0.091374 | 0.0625 | – |
| 4 | 1.125 | 1.1875 | 1.15625 | 0.021743 | 0.03125 | – |
| 5 | 1.125 | 1.15625 | 1.140625 | -0.0119 | 0.015625 | + |
| 6 | 1.140625 | 1.15625 | 1.148438 | 0.004825 | 0.007813 |
8.
a. Given the following data
x | 5 | 6 | 7 | 8 | 9 |
F(x) | 25 | 36 | 49 | 64 | 81 |
b. Using a suitable finite difference approximation, find
- f’(5)
- f’(9)
- deflection y in a simply supported beam with a uniform load q and a tensile axial load T is given by:
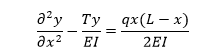
x= location along the beam; T= tension applied; E= Young’s modulus of elasticity of the beam; I= second moment of area; q= uniform load intensity; L= length of the beam.
Given,
T= 30KN, q= 50KN/m, L=10m, E= 35GN/m2 and I= 5.0 × 10-4m4
Using the central difference approximation and a grid size of 2.5m, find the deflection at the center of the beam. Assume no deflection at both ends of the beam.
8a)
ℎ = 9−8 =8−7 = 7−6 = 6−5 = 1
Finite difference approximation is,
𝑓′(𝑥) = (𝑦𝑖+1 − 𝑦𝑖 )/h Forward difference.
𝑓′(𝑥) = (𝑦𝑖−𝑦𝑖−1)/ℎ Backward difference.
- 𝑦𝑖+1 = 36, 𝑦𝑖 = 25
𝑓′(5) = (36−25)/1 = 11 - 𝑦𝑖 = 81, 𝑦𝑖−1 = 64
𝑓′(9) = (81−64) /1 =17
b.
𝜕2𝑦/𝜕𝑥2 – [30×103𝑦 /(35×109)(5.0×10−4)] = [(50×103) 𝑥(10−𝑥)/ 2(35×109)(5×10−4)]
𝜕2𝑦/𝜕𝑥2−1.714×10−3 𝑦=1.428 × 10−3 𝑥(10−𝑥)
𝜕2𝑦/𝜕𝑥2−1.714×10−3 𝑦=1.428 × 10−3 𝑥(10−𝑥)
Approximating the derivative using central difference,
𝜕2𝑦/𝜕𝑥2 ≈ (𝑦𝑖+1−2𝑦𝑖 + 𝑦𝑖−1 )/(Δ𝑥)2
Therefore
[(𝑦𝑖+1−2𝑦𝑖 + 𝑦𝑖−1 )/(Δ𝑥)2 − 1.714×10−3𝑦] = 1.428 × 10−3 𝑥(10−𝑥)
At node 1:
x= 0 and Δ𝑥=2.5
y1= 0…………………..1 (neglecting deflection at both ends).
At node 2:
[(𝑦3−2𝑦2+𝑦1 )]/ (2.5)2 −1.714×10−3𝑦=1.428×10−3(2.5)(10−2.5)
0.16𝑦1−0.3202𝑦2+0.16𝑦3=0.02678……………………….2
At node 3:
0.16𝑦2−0.3202𝑦3+0.16𝑦4 = 0.03572………………………….3
At node 4:
0.16𝑦3−0.3202𝑦4+0.16𝑦5 = 0.02678………………………….4
At node 5:
y5 = 0………………………5 (neglecting deflection at both ends).
Use any method of solving simultaneous equation with iteration.
The solution to the simultaneous equation will be the answer at y3
𝑦1=0
4𝑦1 /25−1601𝑦2 /5000 + 4𝑦3 /25=1339/50000
4𝑦1 /25−1601𝑦3 /5000+4𝑦4 /25= 893/25000
4𝑦3 /25−1601𝑦4 /5000+4𝑦5 /25=1339/50000
𝑦5=0
𝑦1,𝑦2,𝑦3,𝑦4,𝑦5
𝑦1=0
𝑦2=−3572539/12832010=−0.2784083709
𝑦3=−2500893/6416005=−0.38978975234
𝑦4=−3572539/12832010=−0.27840837094
𝑦5=0
Given the following value of a function
| X | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.4 |
|---|---|---|---|---|---|---|
| Y | 2.7183 | 3.3201 | 4.0552 | 6.0496 | 7.3891 | 9.0250 |
Prepare a difference table and evaluate
𝑑𝑦/ 𝑑𝑥 𝑎𝑛𝑑 𝑑 2𝑦/𝑑𝑥2 𝑎𝑡
(𝑖) 𝑥 = 1.2 (𝑖𝑖) 𝑥 = 1.6 (𝑖𝑖𝑖)𝑥 = 2.0
i) At x =1.2 x + h = 1.2 + 0.2 = 1.4 x – h = 1.2 – 0.2 = 1.0
where h = 0.2 𝑦𝑛+ℎ = 4.0552 𝑦𝑛−ℎ= 2.7180
𝑑𝑦/ 𝑑𝑥 = (𝑦𝑛+1 − 𝑦𝑛−1 )/2ℎ
= (4.0552 − 2.7180 )/2 × 0.2 = 3.343
𝑑 2𝑦/ 𝑑𝑥2 = 1 /ℎ2 (𝑦𝑛+ℎ − 2𝑦𝑛−ℎ + 𝑦) = 1 /0.2 2 (4.0552 − 2(2.7180) + 3.3201) = 48.4825
ii)At x =1.6 x + h = 1.6 + 0.2 = 1.8 x – h = 1.6 – 0.2 = 1.4
where h = 0.2 𝑦𝑛+ℎ= 6.0496 𝑦𝑛−ℎ= = 4.0552
𝑑𝑦 /𝑑𝑥 = (6.0496 − 4.0552)/( 2 × 0.2) = 4.986
𝑑 2𝑦 /𝑑𝑥2 = 1 /ℎ2 (𝑦𝑛+ℎ − 2𝑦𝑛−ℎ + 𝑦) = 1 /0.2 2 (6.0496 − 2(4,0552) + 4.9530) = 72.305
iii)At x = 2.0 x + h = 2.0 + 0.2 = 2.2 x – h =2.0 – 0.2 = 1.8
where h = 0.2 𝑦𝑛+ℎ= 9.0250 𝑦𝑛−ℎ= = 6.0496
𝑑𝑦 /𝑑𝑥 = (9.0250 − 6.0496)/ 2 × 0.2 = 7.4385
𝑑 2𝑦 /𝑑𝑥2 = 1/ ℎ2 (𝑦𝑛+ℎ − 2𝑦𝑛−ℎ + 𝑦) = 1/ 0.2 2 (9.0250 − 2(7.4385) + 7.3891) = 38.4275
| X | Y | ΔY | Δ^2Y |
|---|---|---|---|
| 1.0 | 2.7183 | ||
| 1.2 | 3.3201 | 0.6018 | |
| 1.4 | 4.0552 | 0.7351 | 0.1333 |
| 1.6 | 4.9530 | 0.8978 | 0.1627 |
| 1.8 | 6.0496 | 1.0966 | 0.1988 |
| 2.0 | 7.3891 | 1.3395 | 0.2429 |
| 2.2 | 9.0250 | 1.6359 | 0.2964 |
Numerical solution of first order differential equation
a) Solve the following equation by using Taylor’s series method:
𝑑𝑦 /𝑑𝑥 = 𝑥 2𝑦 − 1, 𝑦 = 0 𝑤ℎ𝑒𝑛 𝑥 = 0
𝑓𝑖𝑛𝑑 𝑦 𝑤ℎ𝑒𝑛 𝑥 = 0.03 𝑑𝑦 𝑑𝑥 = 𝑥 2𝑦 − 1 𝑦 = 0 , 𝑤ℎ𝑒𝑛 𝑥 = 0 𝑓𝑖𝑛𝑑 𝑦 𝑤ℎ𝑒𝑛 𝑥 = 0.03
b) Apply picard’s method to obtain the third approximation of all the solution of equation 𝑑𝑦 𝑑𝑥 = 2𝑦 − 2𝑥 2 − 3 𝑔𝑖𝑣𝑒𝑛 𝑡ℎ𝑎𝑡 𝑦 = 2 𝑤ℎ𝑒𝑛 𝑥 = 0
c) Let 𝑑𝑦/ 𝑑𝑥 = 𝑥 + 𝑦 𝑎𝑛𝑑 𝑦 = 1 𝑤ℎ𝑒𝑛 𝑥 = 0 use Euler’s modified method to solve the equation up to four approximation. Obtain y at x = 0.2
Pls remember to put your calculator to radian format.
a)Using Simpson’s rule
log𝑒 𝑥 = ln 𝑥 𝑇ℎ𝑒𝑟𝑒𝑓𝑜𝑟𝑒
𝐼 = ∫ 1.40.2(sin 𝑥 − log𝑒 𝑥 + 𝑒 𝑥 )𝑑𝑥 1.4 0.2
Since n(sub-interval) is not given ; n is assume to be 4 intervals Therefore 𝑛 = 4 , 𝑎 = 0.2 , 𝑏 = 1.4 𝑓𝑟𝑜𝑚 𝑡ℎ𝑒 𝑙𝑖𝑚𝑖𝑡
Therefore 𝑑 = (𝑏−𝑎) /𝑛 = (1.4−0.2)/ 4 = 0.3
Let 𝑓(𝑥) = sin 𝑥 − ln 𝑥 + 𝑒 𝑥
𝑥 = 0.2 𝑓(0.2) = sin(0.2) − ln(0.2) + 𝑒 0.2 = 3.0295
𝑥 = 0.5 𝑓(0.5) = sin(0.5) − ln(0.5) + 𝑒 0.5 = 2.8213
𝑥 = 0.8 𝑓(0.8) = sin(0.8) − ln(0.8) + 𝑒 0.8 = 3.1660
𝑥 = 1.1 𝑓(1.1) = sin(1.1) − ln(1.1) + 𝑒 1.1 = 3.800
𝑥 = 1.4 𝑓(1.4) = sin(1.4) − ln 1.4 + 𝑒 1.4 = 4.7042
| (x) | 0.2 | 0.5 | 0.8 | 1.1 | 1.4 |
|---|---|---|---|---|---|
| f(x) | 3.0295 | 2.8213 | 3.1660 | 3.800 | 4.7042 |
𝐼 = 𝐷/ 2 [𝑓(𝑥1 ) + 2(𝑥2 ) + 𝑓(𝑥3 ) + 𝑓(𝑥4 )) + 𝑓(𝑥5)] = 0.3 2 (3.0295 + 2(2.8213+3.1660+3.800) +4.7042) = 4.0963
Check the answer using normal integration
𝐼 = ∫1.40.2 𝑠𝑖𝑛𝑥𝑑𝑥 − ∫1.40.2 ln 𝑥𝑑𝑥 + ∫1.40.2 𝑒 𝑥 𝑑𝑥
= (− cos(𝑥) − 𝑥 ln 𝑥 + 𝑒 𝑥 )0.2 1.4
=[(− cos(1.4) + cos(0.2) − ((1.4 ln 1.4) − (0.2 ln 0.2)] + (𝑒 1.4 − 𝑒 0.2 ) = 4.0509.
b)Using Simpson’s one to third rule
𝐼 =( 𝑏−𝑎 )/6 [(𝑓(𝑎) + 4𝑓 ( (𝑏+𝑎)/ 2 ) + 𝑓(𝑏)]
𝑏 = 1.4 𝑎 = 0.2 (𝑏+𝑎)/ 2 = 0.8
𝑓 (𝑎) = 𝑓(0.2) = sin(0.2) − ln(0.2) + 𝑒 0.2 = 3.0295
𝑓 (𝑏) = 𝑓(1.4) = sin(1.4) − ln(1.4) + 𝑒 1.4 = 4.7042
𝑓 ( 𝑏+𝑎 2 ) = 𝑓(1.4) = sin(1.4) − ln(1.4) + 𝑒 1.4 = 4.7042
𝐼 = ((𝑏−𝑎) /6) [𝑓(𝑎) + 4𝑓 ( (𝑏+𝑎)/ 2 ) + 𝑓(𝑏)]
𝐼 =[ (1.4 − 0.2)/ 6 ](3.0295 + 4(5.4826) + 4.7042) = 5.9328
C) Simpson three eight rule
| x | 0.2 | 0.5 | 0.8 | 1.1 | 1.4 |
|---|---|---|---|---|---|
| f(x) | 3.0295 | 2.8213 | 3.1660 | 3.800 | 4.7042 |
𝐼 = (3𝐷/ 8) (𝑓(𝑥1 ) + 3(𝑥2 ) + 𝑓(𝑥3 ) + 𝑓(𝑥4 )) + 𝑓(𝑥5))
= 3×0.3 8 (3.0295 + 3(2.8213 + 3.166 + 3.8) + 4.7042) = 4.1737
D) Weddle’s rules can only be solved for n= 6
∫ ba𝑓(𝑥)𝑑𝑥 = (3 /10) 𝐷(𝑓(𝑥o ) + 5𝑓(𝑥1 ) + 𝑓(𝑥2 ) + 6𝑓(𝑥3) + 𝑓(𝑥4 ) + 5𝑓(𝑥5 ) + 2𝑓(𝑥6 ) + 5𝑓(𝑥7 ) + ⋯ )
D= (𝑏−𝑎) /2 = (1.4−0.2) /6 = 0.2
| (x) | 0.2 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|
| f(x) | 3.0295 | 2.8976 | 3.166 | 3.5598 | 4.070 | 4.7042 |
𝐼 = (3 × 0.2 )/10 [3.0295 + 5(2.8976) + 3.166 + 6(3.5598) + 4.070 + 5(4.7042)] = 4.17
Numerical solution of first order differential equation
a) Solve the following equation by using Taylor’s series method:
𝑑𝑦 /𝑑𝑥 = 𝑥 2𝑦 − 1, 𝑦 = 0 𝑤ℎ𝑒𝑛 𝑥 = 0
𝑓𝑖𝑛𝑑 𝑦 𝑤ℎ𝑒𝑛 𝑥 = 0.03
b) Apply picard’s method to obtain the third approximation of all the solution of equation 𝑑𝑦 𝑑𝑥 = 2𝑦 − 2𝑥 2 − 3 𝑔𝑖𝑣𝑒𝑛 𝑡ℎ𝑎𝑡 𝑦 = 2 𝑤ℎ𝑒𝑛 𝑥 = 0
c) Let 𝑑𝑦/ 𝑑𝑥 = 𝑥 + 𝑦 𝑎𝑛𝑑 𝑦 = 1 𝑤ℎ𝑒𝑛 𝑥 = 0 use Euler’s modified method to solve the equation up to four approximation. Obtain y at x = 0.2
Euler’s formula
𝑦1 = 𝑦0 + ℎ𝑓(𝑥0, 𝑦0)
𝑦1 = 𝑦0 + ℎ( 𝑥0 + 𝑦0)
1st Iteration
𝑦0 = 1 𝑥0 = 0 ℎ = 0.2
𝑦1 = 𝑦0 + ℎ( 𝑥0 + 𝑦0 ) = 1 + 0.2 (0 + 1) = 1.2
2 nd Iteration
𝑦0 = 1.2 𝑥0 = 0.2 ℎ = 0.2
𝑦2 = 𝑦0 + ℎ( 𝑥0 + 𝑦0 ) = 1.2 + 0.2 (0.2 + 1.2) = 1.48
3rd Iteration
𝑦0 = 1.48 𝑥0 = 0.4 ℎ = 0.2
𝑦3 = 𝑦0 + ℎ( 𝑥0 + 𝑦0 ) = 1.48 + 0.2 (0.4 + 1.48) = 1.856
4th Iteration
𝑦0 = 1.856 𝑥0 = 0.6 ℎ = 0.2
𝑦4 = 𝑦0 + ℎ( 𝑥0 + 𝑦0 ) = 1.856 + 0.2 (0.6 + 1.856) = 2.3472
Y at x = 0.2 is 1.48.
Credits
Disclaimer
This entire solution may not be 100% accurate, any mistake or typo found should be reported to SmartBukites Management through the following email [email protected] »
All the custom solutions are written for individual research and reference ONLY. SmartBukites does not promote plagiarism in any form and firmly believes that Student will use the solutions models in their individual efforts.
Do you have a Question to Ask?
SmartBukites have a Facebook Group which allows everyone to ask, answer and seek academic help. At SmartBukites, we believe Smart approach to Education will go along way in easing human academic struggle.
Click the link to join now!!! https://web.facebook.com/groups/675122219621351
