a. State the following laws:
i. Faraday’s law, mentioning the conditions in which induction can decor
ii.Lenz’s law
b. In figure Q1, let , and assume that the conductor joining the two ends is perfect and that the magnetic field produced by I(t) is negligible, find
i. Vab(t)
ii.Iab(t)
1a.
i. When a conductor is placed in a time varying field an e.m.f is induced. And the magnitude of the induced e.m.f is directly proportional to the rate of change of flux.
e.m.f = -მϕ/მt (Volts)
- A time changing flux linking a stationary closed path.
- Relative motion between a steady flux and a closed path
- A combination of the two. i.e time changing flux and a motioned closed path.
ii. Lenz’s law state that the direction of the induced e.m.f is always such that it oppose the change that produces it. Therefore the negative sign in the formula is as a result of lenz’s law.
b.
A = l × b
Ø = BA = 0.2 × 0.5 × cos 120πt = 0.05 cos120 πt T
Vab = -მ Ø/მt = – მ(0.05 cos 120πt) / მt = 6π sin120 πt V
Iab = Vab/R = (6π sin120 πt)/R Ω
a) Given that J = ∇ × H, derive the Maxwell’s equation in the tme varying fields.
b) Given A = 26.72 sinx sin3 × 108t ax wb/m in free space, find B and H
a. But divergence of a curl of any vector field is identically zero.
Hence;
∇.(∇×H) = 0 = ∇.J……………………………(i)
But ∇.J = – მ(∇.D)/მt ≠ 0 …………………..(ii)
Eqn (i) and (ii) are not compatible for time varying condition. Therefore they must be modified.
∇ x H = J + Jd
∇ .(∇x H) = 0 = ∇.J + ∇.Jd
∇.Jd = – ∇.J = მ(∇.D)/ მt = ∇.მD/მt
∇ x H = J + მ(∇.D)/ მt
b.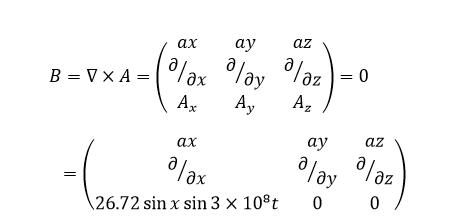
Ay = Az = 0 therefore the determinant of the overall matrix will be zero
B = (0)ax + ( მ(26.72 sinx sin3 × 108t)/ მz – 0 )ay – ( მ(26.72 sinx sin3 × 108t)/ მy – 0)az
B = 0ax + 0ay + 0az
B = μH
H = 0/ μ = 0
a. The H field in free space is given by . Find
i. β ii. λ iii. E(x,t) at P(0.1,0.2,0.3)
b. A lossless material has relative permittivity and permeability with values 9 and 4 respectively. If a uniform plane wave Ex propagates through it in the ay direction and given by, Find
i. β ii. λ iii. Vp iv. Intrinsic impedance
a) The actual wave equation is; 𝐻(𝑥,𝑡)=𝐻0cos(𝜔𝑡−𝜑𝑥).
By comparison, H0 = 30, ω= 107
i. 𝛽=𝜔/𝐶
=107 / 3×108 = 0.033 𝑟𝑎𝑑/𝑚
ii. 𝜆=2𝜋/𝛽
=2𝜋/0.033 = 190.4 𝑚
iii. ∇×𝐻 = 𝜀0 (𝜕𝐸/𝜕t)
= 𝑎𝑧(𝜕𝐻𝑦/𝜕𝑥) = 𝜕(30cos(107𝑡−𝛽𝑥))/𝜕𝑥 𝑎𝑧̅̅̅
cos(𝐴−𝐵)=cos𝐴cos𝐵 − sin𝐴sin𝐵
=𝜕(30cos(107𝑡−𝛽𝑥))/𝜕𝑥 𝑎𝑧̅̅̅
=30 𝜕(cos107𝑡 cos𝛽𝑥 )/𝜕𝑥 𝑎𝑧̅̅̅ + 30 𝜕(sin107𝑡 sin𝛽𝑥 )/𝜕𝑥 𝑎𝑧̅̅̅
=30(−𝛽cos107𝑡 sin𝛽𝑥+𝛽sin107𝑡 cos𝛽𝑥) 𝑎𝑧̅̅̅
=30𝛽(−cos107𝑡 sin𝛽𝑥 + sin107𝑡 cos𝛽𝑥) 𝑎𝑧̅̅̅
=30𝛽(sin107𝑡 cos𝛽𝑥−cos107𝑡 sin𝛽𝑥) 𝑎𝑧̅̅̅
sin(𝐴−𝐵)=sin𝐴cos𝐵−cos𝐴sin𝐵
=30𝛽(sin107𝑡 cos𝛽𝑥−cos107𝑡 sin𝛽𝑥) = 30𝛽sin(107𝑡−𝛽𝑥) 𝑎𝑧̅̅̅
∇×𝐻 = 30𝛽sin(107𝑡−𝛽𝑥) 𝑎𝑧̅̅̅
𝐸=∫((∇×𝐻)/𝜀0) 𝜕𝑡
= ∫(30×0.033sin(107𝑡−𝛽𝑥)) / 8.85×10−12 𝑎𝑧̅̅̅
=∫−11.18cos(107𝑡−0.033𝑥)𝑎𝑧̅̅̅ 𝐾𝑉/𝑚
P(0.1,0.2,0.3) x=0.1, y=0.2 & z =0.3
𝐸(𝑥,𝑡)=−11.18cos(107𝑡−0.033×0.1) = −11.18cos(107𝑡−0.0033)𝑎𝑧̅̅̅ 𝐾𝑉/𝑚
𝐸(𝑥,𝑡)=−11.18cos(107𝑡−0.0033)𝑎𝑧̅̅̅ 𝐾𝑉/𝑚
b)For a lossless medium
𝜀0=8.85×10−12 𝜇𝑜=4𝜋×10−7
i) 𝛽=𝜔√𝜇𝜀
=2𝜋×107√(4×9×4𝜋×10−7×8.854×10−12)
𝛽=1.258𝑟𝑎𝑑/𝑚
ii) 𝜆=2𝜋/𝛽
=2𝜋/1.258
𝜆=5 𝑚
iii) 𝑉𝑝=𝜔/𝛽
=(2𝜋×107 )/1.258 = 4.995×107𝑚/𝑠
iv) ƞ=√(𝜇/𝜀)
=√(4×4𝜋×10−7)/(9×8.854×10−12 )
=251.16 Ω
a. Determine the polarization of the wave if the electric field intensity in a given region is given by
𝐸=(2𝑎𝑥+𝑗3𝑎𝑦)𝑒−0.3𝑧𝑒−𝑗0.6𝑧 𝑉/𝑚
b. A 100 MHz TE polarized wave with amplitude 1.0 V/m is obliquely incident from air (z<0) onto a slab of lossless, nonmagnetic material with (z>0). The angle of incidence is 40o. Calculate
i. The angle of transmission
ii. The reflection and transmission coefficients
iii.The incident, reflected and transmitted E fields
𝐸𝑥(𝑧,𝑡) = 2𝑒−0.3𝑧cos(𝜔𝑡−0.6𝑧)
𝐸𝑦(𝑧,𝑡) = −3𝑒−0.3𝑧sin(𝜔𝑡−0.6𝑧).
In a z= 0 plane, these components become,
1/2𝐸𝑥(0,𝑡) = cos𝜔𝑡……………1
1/3𝐸𝑦(0,𝑡) = −sin𝜔𝑡……………2 Squaring and adding both equations, we get,
1/4𝐸2𝑥(0,𝑡) + 1/9𝐸2𝑦(0,𝑡) = 1
𝐸2𝑥 (0,𝑡)/4 + 𝐸2𝑦(0,𝑡)/9 = 1
Which is an equation of an ellipse. Hence the wave is elliptically polarized. The major axis is along the y- axis and the minor axis is along the x- axis.
b.
i)
𝐸𝑜=1.0𝑣/𝑚
𝜀𝑟=25
𝜃𝑖=400
𝛽1=𝜔/𝑐
=2𝜋(100×106)3×108
𝛽1=2.09𝑟𝑎𝑑/𝑚
𝛽2=𝜔√𝜀𝑟/𝑐
=(2𝜋(100×106)√25) / (3×108)
𝛽2=10.45𝑟𝑎𝑑/𝑚
𝛽1/𝛽2 = 2.09/10.45 = 1/5
𝑓𝑟𝑜𝑚 𝑆𝑛𝑒𝑙𝑙′𝑠 𝑙𝑎𝑤 sin𝜃𝑡=𝛽1/𝛽2
sin𝜃𝑖=1/5sin400 𝜃𝑡
=sin−1(0.2×0.6427)
𝜃t = 7.4𝑜
ii)
𝜂1=120𝜋Ω
𝜂2=𝜂1/√𝜀𝑟
=120𝜋/√25 = 120𝜋/5
𝜂2 = 24𝜋Ω
𝛤𝑇𝐸=(𝜂2cos𝜃𝑖−𝜂1cos𝜃𝑡) / (𝜂2cos𝜃𝑖+𝜂1cos𝜃𝑡)
=(24𝜋cos450 − 120𝜋cos7.40 )/(24𝜋cos450+120𝜋cos7.40 )
𝛤𝑇𝐸=−0.732
𝜏𝑇𝐸=1+𝛤𝑇𝐸
=1 − 0.732
𝜏𝑇𝐸 = 0.268
𝐸𝑠=𝐸𝑜𝑒−𝑖𝛽1(𝑥sin𝜃𝑖−𝑧cos𝜃𝑖)𝑎𝑦 𝑣/𝑚
=1𝑒−𝑖2.09(𝑥sin45−𝑧cos45)𝑎𝑦 𝑣/𝑚
𝐸𝑠=1𝑒−𝑖1.34𝑥𝑒−𝑖1.6𝑧𝑎𝑦 𝑣/𝑚
𝐸𝑠(𝑧,𝑡)=1cos(𝜔𝑡−1.34𝑥−1.6𝑧)
𝑓𝑜𝑟 𝑟𝑒𝑓𝑙𝑒𝑐𝑡𝑒𝑑 𝐸r𝑠=𝛤𝑇𝐸𝐸i𝑜
𝐸r𝑠 =−0.732×1=−0.732
𝐸r𝑠=𝐸r𝑜𝑒−𝑗𝛽1(𝑥sin𝜃𝑖+𝑧cos𝜃𝑖)𝑎𝑦 𝑣/𝑚
𝐸r𝑠=−0.732𝑒−𝑗1.34𝑥𝑒𝑗1.6𝑧𝑎𝑦 𝑣/𝑚
𝐸𝑟(𝑧,𝑡)=−0.732cos(𝜔𝑡−1.34𝑥+1.6𝑧)
𝑓𝑜𝑟 𝑡𝑟𝑎𝑛𝑠𝑚𝑖𝑡𝑒𝑑 𝐸t𝑜=𝜏𝑇𝐸𝐸i𝑜
𝐸t𝑜 =0.268×1= 0.268
𝐸t𝑠 = 𝐸t𝑜𝑒−𝑗𝛽2(𝑥sin𝜃𝑡+𝑧cos𝜃𝑡)𝑎𝑦 𝑣/𝑚
𝐸t𝑠 = 𝐸t𝑜𝑒−𝑗10.45(𝑥sin7.4+𝑧cos7.4)𝑎𝑦 𝑣/𝑚
𝐸t𝑠 = 0.268𝑒−𝑗1.35𝑥𝑒−𝑗10.4𝑧𝑎𝑦 𝑣/𝑚
𝐸𝑡(𝑧,𝑡) = 0.268cos(𝜔𝑡−1.35𝑥−10.4𝑧)
a.
i. Show that for quarter wavelength transmission line.
𝑍𝑖𝑛=𝑍2𝑂𝑇 /𝑍𝑙
ii. Show that for half wavelength transmission line
Zin = Zl
b. A 100m long lossless transmission line has a total inductance and capacitance of 27.72μH and 18nF, respectively. Determine
i. The velocity of propagation and the phase constant for an operating frequency of 100kHz and
ii. The characteristic impedance of the transmission line
a.
i)
𝑍𝑖𝑛(0)=𝑍𝑂𝑇 ( (𝑍𝑙+𝑗𝑍𝑂𝑇 tan(𝛽𝑙))/( 𝑍𝑂𝑇+𝑗𝑍𝑙 tan(𝛽𝑙)) )
But β= 2π/λ and for quarter wavelength l= λ/4. On substituting
𝑍𝑖𝑛(0)= 𝑍𝑂𝑇 [ (𝑍𝑙+𝑗𝑍𝑂𝑇tan(2π/λ × λ/4))/( 𝑍𝑂𝑇+𝑗𝑍𝑙tan(2π/λ × λ/4) ]
𝑍𝑖𝑛=𝑍2𝑂𝑇 /𝑍𝑙
ii) For half wavelength l= λ/2. Therefore,
𝑍𝑖𝑛(0)= 𝑍𝑂𝑇 [(𝑍𝑙+𝑗𝑍𝑂𝑇tan(2π/λ × λ/2))/( 𝑍𝑂𝑇+𝑗𝑍𝑙tan(2π/λ × λ/2) ]
𝑍𝑖𝑛=𝑍𝑙
b)
i)
𝐿𝑙=27.72×10−6 /100= 0.2772 𝜇𝐻/𝑚
𝐶𝑙=18×10−9 /100=0.18 𝑛𝐹/𝑚.
The velocity of propagation is
𝑈𝑝=1/√(𝐿𝑙𝐶𝑙)
= 1/√(0.2772×10−6×0.18×10−9 )
𝑈𝑝 =1.416×108 𝑚/𝑠
And the propagation constant is,
𝛽=𝜔/𝑈𝑝
=(2𝜋×100×103 )/(1.416×108)=4.439×10−3 𝑟𝑎𝑑/𝑚
ii)
𝑍=√(𝐿𝑙/𝐶𝑙)
=√(0.2772×10−6 / 0.18×10−9 )
𝑍 =39.234 Ω
a. State four solutions to microwave problems using smith chart
b. In a rectangular waveguide with dimension a=1.5 cm, b=0.8 cm, σ=0, μ=μ0, ε=4ε0, find:
𝐻𝑥=2sin(𝜋𝑥/𝑎) cos(3𝜋𝑦/𝑏) sin(𝜋×1011𝑡−𝛽𝑧) 𝐴/𝑚
i. The mode of operation ii. The cut-off frequency iii. The phase constant
iv. The propagation constant v. The intrinsic wave impedance
a.
i. plotting a complex impedance
ii. finding VSWR for a given load.
iii. finding the admittance
iv. finding the input impedance of a transmission line terminated in a short or open.
b.
i) By comparing the given equation with
𝐻𝑥=𝐻𝑜sin(𝑚𝜋𝑥/𝑎) cos(𝑛𝜋𝑦/𝑏) sin(𝜔𝑡−𝛽𝑧).
m= 1 and n= 3.
Therefore the mode of operation is 𝑇𝑀13.
ii) 𝐻𝑥=2sin(𝜋𝑥/𝑎) cos(3𝜋𝑦/𝑏) sin(𝜋×1011𝑡−𝛽𝑧) 𝐴/𝑚
ω= 2πf = π×1011 (from the given equation) therefore
f= 5×1010 Hz
𝑓𝑐13=1/(2𝜋√𝜇𝜀) × √[(𝑚𝜋/𝑎)2+(𝑛𝜋/𝑏)2 ]
since μ=μ0,ε=4ε0
=1/(2𝜋√4ε0μ0) × √[(𝜋/0.015)2+(3𝜋/0.008)2 ]
=√[(209.44)2+(1178.097)2 ] / [2𝜋√(4×8.854×10−12×4π×10−7 )]
=(√1431777.655) /4.1916×10−8
=1196.569 / 4.1916×10−8 =285.468×108
𝑓𝑐13=28.57𝐺𝐻𝑧
iii) 𝛽=(𝜔√𝜇𝜀) × √(1−(𝑓𝑐 /𝑓)2 )
=(π×1011√4ε0μ0) × √[1−(28.5468×109 / 50×109)2] = 6.6712×10−9×𝜋×1011(0.82099)
=2095.8×0.82099
𝛽=1719.98 𝑟𝑎𝑑/𝑚
iv) 𝛾=𝑗𝛽
𝛾 =𝑗1719.98 𝑚−1
v) ƞ=ƞ′√[1−(𝑓𝑐/𝑓)2 ]
ƞ′=√𝜇𝜖=√𝜇𝑜4𝜀𝑜
ƞ′=188.37 Ω
ƞ =188.37×√[1− (28.5468×109 /50×109)2 ]
=188.37×0.82099
ƞ =154.6 Ω
a.Prove that for an isotropic radiator, the electric field at a distance R from the isotropic antenna is given by
𝐸 =√(60𝑃𝑡 /𝑅)
b. The amplitude of the electric field intensity broadside to a half-wave dipole antenna at a distance of 12km is 0.2V/m in free space. If the operating frequency is 75 MHz, determine:
i. The length of the antenna
ii.The total power that it radiates
iii. Write the general expressions for the electric and magnetic field intensities in the time domain
a. since the power density of an isotropic radiated wave is inversely proportional to the distance r from the source then
𝑃𝑑=𝑃𝑡/4𝜋𝑅2
The electric field intensity at a distance r away from the source is in free space is
𝐸=√(𝑃𝑑𝑍𝑜 )
Therefor;
=√(𝑃𝑡120𝜋/4𝜋𝑅2 )
𝐸 =√(60𝑃𝑡 /𝑅)
b.
𝑓=75 𝑀𝐻𝑧
𝜔=2𝜋𝑓 =471.239 𝑀𝑟𝑎𝑑/𝑠
𝛽 = 𝜔𝑐
𝛽 = 471.239×106 × 3×108 =1.57 𝑟𝑎𝑑/𝑚
i) 𝜆=2𝜋𝛽 =2𝜋×1.57=4 𝑚
𝐸=(𝐼𝑜 /2𝜋𝑟)ƞ𝑜 Therefore 𝐼𝑜=2𝜋𝑟/ƞ0
𝐸=((2𝜋×12×103 )/120𝜋)×0.2
𝐸 =40 𝐴
𝑅=(1.219 / 2𝜋) ƞ𝑜
=(1.219/2𝜋)×120𝜋
𝑅 =73.14 Ω
ii) 𝑃𝑟𝑎𝑑=1/2𝐼2𝑜𝑅
=0.5×402×73.14
𝑃𝑟𝑎𝑑 =58.512 𝐾𝑤
iii)
𝐸𝜃(𝑟,𝜃,∅,𝑡)=(−ƞ𝑜𝐼𝑜 /2𝜋𝑟)[cos(𝜋/2cos𝜃) / sin𝜃] sin(𝜔𝑡−𝛽𝑟)
𝐻𝜃(𝑟,𝜃,∅,𝑡)=(−𝐼𝑜 / 2𝜋𝑟)[cos(𝜋/2cos𝜃)/sin𝜃]sin(𝜔𝑡−𝛽𝑟).
Substitute the values found in the above equations.
𝐸𝑠=1𝑒−𝑖1.34𝑥 𝑒−𝑖1.6𝑧 𝑎𝑦 𝑣/𝑚
𝐸r𝑠=−0.732𝑒−𝑗1.34𝑥 𝑒−𝑗1.6𝑧 𝑎𝑦 𝑣/𝑚
𝐸t𝑠=0.268𝑒−𝑗1.35𝑥 𝑒−𝑗10.4𝑧 ay𝑣/𝑚
Disclaimer
This entire solution may not be 100% accurate, any mistake or typo found should be reported to SmartBukites Management through the following email [email protected] »
All the custom solutions are written for individual research and reference ONLY. SmartBukites does not promote plagiarism in any form and firmly believes that Student will use the solutions models in their individual efforts.
Do you have a Question to Ask?
SmartBukites have a Facebook Group which allows everyone to ask, answer and seek academic help. At SmartBukites, we believe Smart approach to Education will go along way in easing human academic struggle.
Click the link to join now!!! https://web.facebook.com/groups/675122219621351
