a) What is fluid?
b) The general relation between shear stress and velocity gradient of a fluid can be written as
τ = M (δu/δy)r + N
Where M, N and r are constant. Comment on the value of the constant so that the fluid may behave as ideal.
c) The velocity distribution over a plate is given by
u = (3/2) y – ½ y2
Where u= velocity (m/s) and y= distance in meter from the plate boundary. If the viscosity of the fluid is 8 poise. Find the shear stress at the plate boundary and at y= 0.15 m. from the plate (1 poise = 0.1 Ns/m2)
a) Fluid is any material that is capable of flowing, it is either liquid or gas and has the ability of continuously deforming under the action of shear force, it can be ideal and it can be real fluid.
Some general properties of fluid include viscosity, compressibility, surface tension, density and specific gravity.
b) The general relationship between shear stress and velocity gradient of a fluid can be written as
τ = M (δu/δy)r + N
Ʈα(du/dy), where the constant of proportionality is (μ) viscosity.
Ʈ = μ(du/dy)
Comparing with the given equation
M = μ , r = 1 and N = 0
Therefore, for ideal fluid, it has no viscosity therefore μ = 0
M = μ = 0 and r = 1
c)
Given u = (3/2)y – (½)y2
and u = 8 poise = 0.8 NS/m2
(du/dy) = (3/2) – y
The velocity gradient du/dy.
At the boundary y = 0
(du/dy)y=0 = (3/2)S-1
At 0.15m from the plate
(du/dy)y=0.15 = (3/2) – 0.15
= 1.35 m/s2
Ʈ = μ(du/dy) = 0.8 x 1.35 = 1.08 N/m2
a) For a place that is at higher level than the mean sea, how will the local atmospheric pressure compare with atmospheric pressure at mean sea level
b) For a very small wedge-shaped element as shown in fig. Q2 (ii). Show that the intensity of pressure is the same in all direction.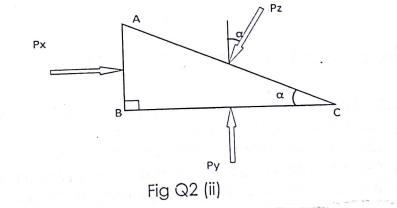
d) Find the difference in pressure between point A and B in fig. Q2 (iii). Neglect weight of air.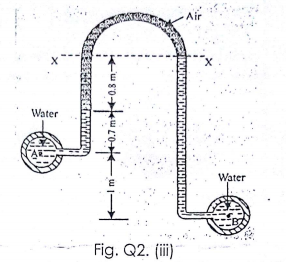
a) It is known that pressure increase as the height is gone deep down, i.e. pressure increase with going down the height, while it decrease if we tend to go up. (Due to corresponding decrease or increase of the column of air standing, respectively).
Therefore if we go higher than sea level, the pressure will be low compared to the atmospheric pressure at the mean sea level.
b) For a very small wedge shared element as shown. If the pressure intensity is the same in all direction. Then
P =F/A Fx =Px AB
Fy= Py BC Fz= Pz AC
Horizontal Forces
Fx = Fz sinα = 0
Fx = Fz sinα
Px AB = Pz sinα AC
But AB = AC sinα
Px sinα AC = Pz sinα AC
Px = Pz
Vertical Forces
Fy = Fz cosα = 0
Py BC = Pz cosα AC = 0
Py BC = Pz AC cosα
But BC = AC cosα
Py AC cosα = Pz AC cosα
Py = Pz
Therefore the pressure intensity is the same in all direction [Px=Py=Pz]
c) To determine the change in pressure.
PA = PB
In part A there’s water + Air, while in B it’s water alone.
ρw gha + ρa gha = ρw ghw
In respect to specific gravity
Sw gha + Sa gha = Sw ghw
Neglecting the weight of air Sa =0
Sw gha = Sw ghw
Therefore the difference in height for
Pb – Pa » hb – ha
hb – ha = (0.8 + 0.7 +1) – 0.7 = 1.8m
But P = ρgh = 1000 × 9.81 × 1.8 = 17.66 KN/m2
a) Determine the total pressure and center of pressure of an isosceles triangular plate of base 4m and an altitude of 4m when it is immerse vertically in an oil of specific gravity 0.9. The base of the plate coincides with the free oil surface.
a)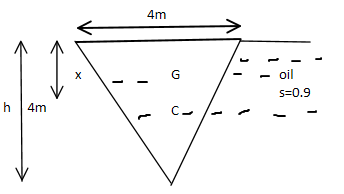
Base of the plate b = 4m
Height of the plate h = 4m
Area = ( ( b x h )/ 2 ) = ( ( 4 x 4 )/ 2 ) = 8 m2
Specific gravity of oil s = 0.9
X = h/3 = 4/3 = 1.33 m
The total pressure on the plate
P = OWAX = ( 0.9 x 9.81 ) x 8 x 1.33
P = 93.94 KN / m2
Centre of pressure
h̅ = ( Ia / AX̅ ) + X̅ = [ ( bh3/36 ) / AX̅ ) ] + X̅
h̅ = [ (4 x 43/36) / 8 x 1.33 ] + 1.33 = 1.998 m
a) Explain how provision can be made in Bernoulli’s equation for a loss of energy occurring between two points in a stream of liquid.
b) A conical tube is fixed vertically with its smaller end upwards. The velocity to flow down the tube is 4.5 m/s at the upper end and 1.5 m/s at the lower end. The tube is 1.5m long and the pressure head at the upper end is 3m of the liquid. The loss in the tube expressed as a head is where v1 and v2 are the velocities at the upper and lower end. What is the pressure head at the lower end?
a) Bernoulli’s equation was based on the assumption of that fluid is non-viscous and therefore frictionless. But practically, all fluids are real and therefore, to be taken into consideration in the application of Bernoulli’s equation, it gets modified by introducing a loss of energy between the two sections of the pipe.
P1/ρg + V12 /2g + Z1 = P2/ρg + V22 /2g + Z2 + h1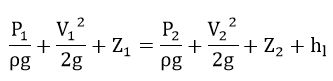
Where hl= loss of energy between the two point.
b)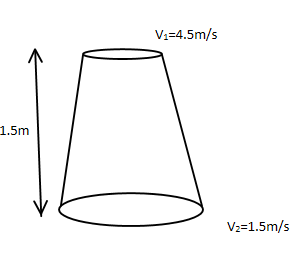
P1 /ρg = 3m
h1 = 0.3(V1 – V2)2/2g = 0.3(4.5 – 1.5)2/(2 × 9.81) = 0.138m
z1 = 0
z2= 1.5m
P1/ρg + V12 /2g + Z1 = P2/ρg + V22 /2g + Z2 + h1
3 + 4.52/(2×9.81) + 0 = P2/ρg + 1.52 /(2×9.81) + 1.5 + 0.138
P2/ρg = 4.033 – 1.753 = 2.28m
a) Develop an expression for the quantity of liquid flowing over a shape-edge v-notch of total angle 2ϴ. In terms of head H above the notch, the angle ϴ, and the coefficient of discharge Cd, assuming the velocity of approach to be small.
b) If the rate of flow of water over a v-notch having ϴ= 35o is 42.5 dm3/s, find the head in centimeter, take Cd as 0.62.
a)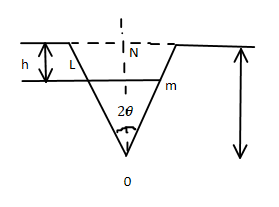
Discharge Q = AV , and V = √ (2gh)
Let the length LM be x
A = xꝺh, To find x, half the triangle LMO is used
tanθ = ( LN/ON ), but ON = H – h
therefore tan θ = ( LN / (H – h) )
LN = ( H – h ) tan θ and x = LM = 2LN = 2( H – h ) tan θ
Area A = xdh
Discharge Q = AV, and V = √ (2gh)
A = 2 ( H – h ) tan θ ꝺh
Q = AV = √ (2gh) x 2 ( H – h ) tan θ ꝺh
But for the actual discharge, coefficient of discharge Cd is introduced.
Therefore
Q = Cd √ (2gh) x 2 ( H – h ) tan θ ꝺh
Q = 2 Cd x √ (2gh) x tan θ x ( H – h ) h½ ꝺh
Integrating the area from 0 to H
Q = 2 Cd x √ (2g) x tan θ ∫H0 ( H – h ) h1/2 ꝺh
Q = 2 Cd √ (2g) tan θ x [ ( (Hh3/2) / 3/2 ) – ( h5/2 / 5/2 )] limit H to 0
Q = 2 Cd √ (2g) tan θ [ ( (2H5/2) / 3 ) – ( (2H5/2) / 5 )]
Q = 2 Cd √ (2g) tan θ H5/2 [ ( 10 – 6 ) / 15 ]
Q = 2 Cd √ (2g) tan θ H5/2 x (4/15)
Q = ( 8 / 15 ) Cd H5/2 √ (2g) tan θ
For a triangle v – notch , θ = ( θ / 2)
b) To find the head of water for a v-notch
θ = 35ᵒ, Q = 42.5 dm3/s = 0.0425 m3/s and Cd = 0.62
Q = ( 8 / 15 ) Cd H5/2 √ (2g) tan θ
H5/2 = (15Q) / (8Cd√ (2g) tan θ)
H5/2 = [ ( 15 X 0.0425 ) / 8 X 0.62 X (√ (2 X 9.81) tan(35/2) ] = 0.092
H = 2√ 0.0925 = 0.00257 m = 0.257 cm
a) What is meant by continuity of flow and what condition does it occur?
b) Oil flow through a pipeline in the figure below which contracts from 450mm diameter of A to 300mm diameter of B and then forks, one branch being 150mm diameter discharge at C and the other branch is 225mm diameter discharge at D. if the velocity at A is 1.8 m/s and the velocity at D 3.6 m/s, what will be discharge of C and D and the velocities of B and C?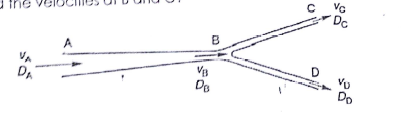
a) Continuity of flow is based on the law of conservation, That is, for a constant flow in a pipe having different diameters in the end, the amount of fluid that enters is the amount of fluid that will leave.
It occurs under constant density (incompressible) condition.
b)
Da= 450mm= 0.45m Va= 1.8 m/s
Db= 300mm= 0.30m Vb= ?
Dc= 150mm= 0.15m Vc= ?
Dc= 225mm= 0.225m Va= 3.6 m/s
Qc= ? and Qd=?
Q= AV and A = πD2/4
Hence;
Aa = π(0.45)2 /4 = 0.159m2
Ab = π(0.30)2 /4 = 0.071m2
Ac = π(0.15)2 /4 = 0.018m2
Ad = π(0.225)2 /4 = 0.0398m2
From continuity equation,
Qa = Qb
AaVa = AbVb
making Vb subject of the formula
Vb = AaVa/Ab = (0.159 x 1.8)/0.071 = 4.031 m/s
Qb = Qc + Qd
AbVb = AcVc + AdVd
collecting like terms and making Vc subject
Vc = (AbVb – AdVd )/ Ac
= [0.071(4.031) – 0.0398(3.5)]/0.018 = 7.94m/s
Qc = AcVc = 0.018(7.94) = 0.143 m3/s
Qd = AdVd = 0.0398(3.6) = 0.143 m3/s
a) A jet of water from 20 mm diameter nozzle is desired vertically upwards. Assuming that the jet remains circular and neglecting any loss of energy, what will be the diameter of the jet at a point 5 m above the nozzle if the velocity with which the jet leaves the nozzle is 10 m/s
b) Write short note on the following
- Stream line
- Stream tube
- Lamina flow
- Turbulent flow
a) Nozzle
𝑑1=20𝑚𝑚=0.02𝑚
𝑣1=10𝑚/𝑠
Δ𝑍=5𝑚
𝑑2=?
𝑣2=?
𝑍1 + V21/2𝑔 + 𝑃1/𝜌𝑔 = 𝑍2 + 𝑉22/2𝑔 + 𝑃2/𝜌𝑔
𝑠𝑖𝑛𝑐𝑒 𝑝 𝑎𝑛𝑑 𝜌 𝑎𝑟𝑒 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡,𝑤𝑒 ℎ𝑎𝑣𝑒
𝑍1 − 𝑍2 = (𝑉21 − 𝑉22) / 2𝑔
𝑉21− 𝑉22 = −2𝑔Δ𝑧
𝑉22= 𝑉21 − 2𝑔Δ𝑧
=102 – 2 × 9.81 × 5
𝑉22 = 1.9
𝑣2=1.378𝑚/𝑠.
𝑛𝑜𝑤 𝐴1𝑉1 = 𝐴2𝑉2
𝜋𝑑21/4 (𝑣1) = 𝜋𝑑22/4 (𝑣2)
𝑑21 𝑣1 = 𝑑22 𝑣2
𝑑2 =√ 𝑑21𝑣1/𝑣2 = 0.022 × 10 /1.378 = 0.05338
= 53.8𝑚𝑚
b)
- Streamline: is the path of imaginary particles in a fluid that came along with it. Each particle in a fluid follows a path called path lines, at any given instant of time, the positions of successive particles can be joined by a curve tangential to the direction of motion of the particle to form a streamline.
- Stream tube: Is formed by drawing streamlines through every point on the circumference of a small area. Stream tubes are used when dealing with flow of large body of fluid.
- Laminar flow: Is a flow in which the particles of the fluid move in an orderly manner and retain the relative position in successive cross sections
- Turbulent flow: Is a flow in which the particles move in a disorderly manner, occupying different relative positions in successive cross sections.
a) A fluid of a constant density flows at the rate of 10 L/s along a pipe AB of 100 mm diameter. The pipe branches at B into two pipes BC and BD each of 25 mm diameter and a third pipe BE and the velocity through BD is 4 m/s. find the flow rates in cm3 of the three branches BC, BD and BE and the velocities in pipes AB, BC and BE
b) Derive the expression for time for emptying tanks
c) State Bernoulli’s Equation
a)
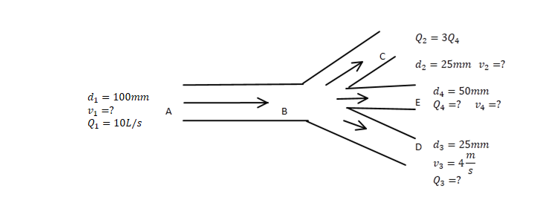
We know 𝑄1 = 𝑄2 + 𝑄3 + 𝑄4 𝑄 = 𝐴𝑉 Note: 1L =1000𝑐𝑚3
𝐵→𝐷
𝑄3 = 𝐴3𝑉3 = ( 𝜋𝑑23 / 4 ) × 𝑣3 = (𝜋 × 0.0252 / 4 ) × 4 = 1.96 × 10−3 𝑚3 /𝑠
=1963.5 × 𝑐𝑚3/𝑠
𝐴→𝐵
𝑄1 = 10𝐿/ 𝑠 = 10000𝑐𝑚3 /𝑠 = 0.01𝑚3/𝑠
𝑄1 = 𝐴1𝑉1
𝑉1= 𝑄1 /𝐴1 = 𝑄1 / 𝜋𝑑21 / 4 = 0.01/ 𝜋0.12 / 4 = 1.27𝑚/𝑠
Now 𝑄1 = 𝑄2 + 𝑄3 + 𝑄4
𝑏𝑢𝑡 𝑄2 = 3𝑄4
→ 𝑄1 = 3𝑄4 + 𝑄3 + 𝑄4
𝑄1 − 𝑄3 = 4𝑄4 , 𝑄4 = 𝑄1 − 𝑄3 / 4 = 10000 − 1963.5 / 4 = 2009𝑐𝑚3/s = 2.009×10−3 𝑚3/𝑠
𝐵→𝐸
𝑄4 = 𝐴4 𝑉4
𝑉4 = Q4 / 𝐴4 = 2.009×10−3 / 𝜋×0.05.2 / 4 =1.023𝑚/𝑠
𝐵→𝐶
𝑄2 = 3𝑄4 = 3 × 2009 = 6027𝑚3 /𝑠
𝑉2 = 𝑄2 𝐴2 = ( 6.027×10−3 / 𝜋×0.025.2/ 4 ) = 12.23𝑚/𝑠
b) Time for empty tanks.
If he consider a tank of uniform cross sectional area A, with an orifice of area at the bottom, let the head of water over the orifice fall from in an interval of T seconds
At any instant of time, let the head of water be after interval of dt seconds, the level will have fallen by dH.
𝑄 = 𝐴𝑑ℎ = 𝑐𝑑 𝑎√2𝑔ℎ 𝑑𝑡
𝑑𝑡= 𝐴 / 𝑐𝑑 (𝑎√2𝑔) ℎ−12 𝑑ℎ
By taking integral from 𝐻2 𝑡𝑜 𝐻1
𝑇= (𝐴 /𝑐𝑑 (𝑎√2𝑔) ) ∫ℎ−12 𝑑ℎ limit 𝐻2 to 𝐻1
T= (2𝐴 / 𝑐𝑑 ( 𝑎√2𝑔)) (√𝐻1−√𝐻2)
c) Bernoulli’s Equation. States that the total energy of each particle of a fluid is the same provided that no energy enters or leaves the system at any point.
𝐻=𝑍 + p / 𝜌𝑔 + 𝑉2 / 2𝑔 = 𝐶𝑜𝑛𝑠𝑡𝑎𝑛𝑡.
a) State pascal’s law
b) Show that the intensity of pressure at a point in a state fluid is the same in all directions
a. Pascal law states that a change in pressure at any point in an enclosed fluid at rest is transmitted uniformly in all directions.
b.
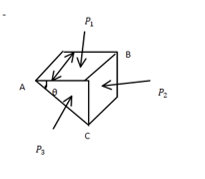
𝑓𝑜𝑟𝑐𝑒 𝑜𝑛 𝐴𝐵 = 𝑃1 × 𝐴𝐵 × 𝑆
𝑓𝑜𝑟𝑐𝑒 𝑜𝑛 𝐵𝐶 = 𝑃2 × 𝐵𝐶 × 𝑆
𝑓𝑜𝑟𝑐𝑒 𝑜𝑛 𝐴𝐶=𝑃3 × 𝐴𝐶 × 𝑆
If the fluid is at rest, these forces are in equilibrium and perpendicular to the forces on which they act.
Resolving theoretically
𝑃1 × 𝐴𝐵 × 𝑆 = 𝑃3 × 𝐴𝐶 × 𝑆𝑐𝑜𝑠𝜃
𝑏𝑢𝑡 𝐴𝑐𝑜𝑠𝜃 = 𝐴𝐵.
𝑃1 = 𝑃3
Similarly . 𝑃2 × 𝐵𝐶 × 𝑆 = 𝑃3 × 𝐴𝐶 × 𝑆 × 𝑆𝑖𝑛𝜃
𝑎𝑙𝑠𝑜, 𝐴𝑐𝑜𝑠𝜃 = 𝐵𝐶
𝑃2 = 𝑃3
𝑃1 = 𝑃2 = 𝑃3
c) 𝑙 = 400𝑚 , 𝑑 = 200𝑚𝑚 = 0.2𝑚 , 𝑓=0.005
𝑄 = 42𝑑𝑚3/𝑠 , 1 𝑑𝑚3 = 1×10−3𝑚3
𝑄 = 42×10−3𝑚3/𝑠
ℎ =? ,
ℎ = ƒ (𝐿 / 𝐷 )( 𝑉2/2𝑔 ) 𝑏𝑢𝑡 𝑄 = 𝐴𝑉 = 𝑉 = 𝑄/𝐴
𝑉 ( 𝑄/𝜋𝑑2 /4 ) = ( 42×10−3 / 𝜋×0.22 / 4 ) = 1.34𝑚/𝑠
ℎ = ( 0.005 × 400 × 1.342 / 0.2 × 2 × 9.81) = 0.915𝑚
a) Write a short note on the following
- Piezometer
- U-tube manometer
- Discharge
- Mean velocity
b) A U – tube manometer is used to measure the gauge pressure of a fluid P of density ρ = 800kgm-3. If the density of the liquid Q is 13 × 103 kgm-3, what will be the gauge pressure at A if h1 = 500 mm and h2 =900 mm
a)
i. Piezometer is a device used to measure liquid pressure by measuring the height to which a column of the liquid rises against gravity.
ii. U-tube manometer consists of a tube of glass bent into a U shape and filled with liquid. The density of the fluid determines the range of pressures that can be measured. It is used to measure gauge pressure as well as differential pressure.
iii. Discharge refers to the volumetric flow rate of a fluid usually in 𝑚3/𝑠 that passes through a given cross section.
iv. Mean velocity: Is the velocity obtained by dividing the rate of a flow of a fluid at a particular point by the cross sectional area at that point.
b)
𝜌= 800𝑘𝑔/𝑚3 , Ø = 13×103𝑘𝑔/𝑚3 ℎ1 = 500𝑚𝑚 ℎ2 = 900𝑚𝑚
𝑃𝐴 = ?
𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝑎𝑡 𝐵 = 𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝑎𝑡 𝐶 𝑃𝐵 = 𝑃𝐶
𝐿𝑒𝑓𝑡𝑙𝑖𝑚𝑏
𝑃𝐵 = 𝑃𝐴 + 𝜌𝑔 ℎ1
𝑅𝑖𝑔ℎ𝑡𝑙𝑖𝑚𝑏
𝑃𝐶 − 𝑃𝐷 + 𝜌𝑚𝑔 ℎ2 𝑃𝐷 = 𝑎𝑡𝑚 𝑝𝑟𝑒𝑠𝑠𝑠𝑢𝑟𝑒 𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑧𝑒𝑟𝑜 𝑤ℎ𝑒𝑛𝑐𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔𝑔𝑎𝑢𝑔𝑒𝑝𝑟𝑒𝑠𝑠𝑢𝑟𝑒
𝑃𝐶 = 𝜌𝑚𝑔 ℎ2
𝑠𝑖𝑛𝑐𝑒 𝑃𝐵 = 𝑃𝐶
𝑃𝐴 + 𝜌𝑔 ℎ1 = 𝜌𝑚𝑔 ℎ2
𝑃𝐴 = 𝜌𝑚𝑔 ℎ2 − 𝜌𝑔 ℎ1
𝑃𝐴 = 13 × 103 × 9.81 × 0.9 – 800 × 9.81 × 0.5 = 110853
= 110.853×103𝐾𝑁/𝑚2
a) Show that the actual discharge out of a small orifice is
b) What is the maximum Gauge pressure of water that can be measured by a piezometer height 20cm and liquid with a relative density of 8.5? (Density of water 1000 kg/m3)
a)
i. Piezometer is a device used to measure liquid pressure by measuring the height to which a column of the liquid rises against gravity.
ii. U-tube manometer consists of a tube of glass bent into a U shape and filled with liquid. The density of the fluid determines the range of pressures that can be measured. It is used to measure gauge pressure as well as differential pressure.
iii. Discharge refers to the volumetric flow rate of a fluid usually in 𝑚3/𝑠 that passes through a given cross section.
iv. Mean velocity: Is the velocity obtained by dividing the rate of a flow of a fluid at a particular point by the cross sectional area at that point.
b)
𝜌= 800𝑘𝑔/𝑚3 , Ø = 13×103𝑘𝑔/𝑚3 ℎ1 = 500𝑚𝑚 ℎ2 = 900𝑚𝑚
𝑃𝐴 = ?
𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝑎𝑡 𝐵 = 𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝑎𝑡 𝐶 𝑃𝐵 = 𝑃𝐶
𝐿𝑒𝑓𝑡𝑙𝑖𝑚𝑏
𝑃𝐵 = 𝑃𝐴 + 𝜌𝑔 ℎ1
𝑅𝑖𝑔ℎ𝑡𝑙𝑖𝑚𝑏
𝑃𝐶 − 𝑃𝐷 + 𝜌𝑚𝑔 ℎ2 𝑃𝐷 = 𝑎𝑡𝑚 𝑝𝑟𝑒𝑠𝑠𝑠𝑢𝑟𝑒 𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑧𝑒𝑟𝑜 𝑤ℎ𝑒𝑛𝑐𝑜𝑚𝑝𝑢𝑡𝑖𝑛𝑔𝑔𝑎𝑢𝑔𝑒𝑝𝑟𝑒𝑠𝑠𝑢𝑟𝑒
𝑃𝐶 = 𝜌𝑚𝑔 ℎ2
𝑠𝑖𝑛𝑐𝑒 𝑃𝐵 = 𝑃𝐶
𝑃𝐴 + 𝜌𝑔 ℎ1 = 𝜌𝑚𝑔 ℎ2
𝑃𝐴 = 𝜌𝑚𝑔 ℎ2 − 𝜌𝑔 ℎ1
𝑃𝐴 = 13 × 103 × 9.81 × 0.9 – 800 × 9.81 × 0.5 = 110853
= 110.853×103𝐾𝑁/𝑚2
Disclaimer
This entire solution may not be 100% accurate, any mistake or typo found should be reported to SmartBukites Management through the following email [email protected] »
All the custom solutions are written for individual research and reference ONLY. SmartBukites does not promote plagiarism in any form and firmly believes that Student will use the solutions models in their individual efforts.
Do you have a Question to Ask?
SmartBukites have a Facebook Group which allows everyone to ask, answer and seek academic help. At SmartBukites, we believe Smart approach to Education will go along way in easing human academic struggle.
Click the link to join now!!! https://web.facebook.com/groups/675122219621351
