Engineering Mathematics II (EGR2302)

Question 1

a. Given that
Ø = 2x² yz³    determine ∇.∇∅

b. Find the first four terms of the Maclaurin’s series expansion  for f(x) = sin2x

Solution

a) Solving divergence of a gradient we integrate the expression twice

∇∅ = (∂2x² yz³)/∂x I + (∂2x² yz³)/∂y j + (∂2x² yz³)/∂z k
=4xyz³ i + 2x² z³ j + 6x² yz² k.

∇.∇∅ = (∂4xyz³)/∂x I + (∂2x² z³)/∂y j + (∂6x² yz²)/∂z                           =4yz³ + 12x²yz
Note; the divergence of a gradient is always a Scalar Quantity

b. Firstly you have to find from 1st – 7th of f(x) and equate it to zero(0):
f(x)= sin 2x           f(0)= sin 2(0)= 0
fⁱ(x)= 2 cos2x        fⁱ(0)= 2 cos2(0)= 2
fⁱⁱ(x)= -4 sin2x       fⁱⁱ(0)= -4 sin2(0)=0
fⁱⁱⁱ(x)= -8 cos2x      fⁱⁱⁱ(0)= -8 cos2(0)=-8
f^iv(x)= 16 sin2x      f^iv(0)= 16 sin2(0)=0
f^v(x)= 32 cos2x      f^v(0)= 32 cos2(0)=32
f^vi(x)= -64 sin2x     f^vi(0)= -64 sin2(0)=0
f^vii(x)= -128 cos2x  f^vii(0)= -128 cos2(0)=-128

f(x)=f(0)+xf’ (0)+x²/2! f” (0)+x³/3! f”’ (0)+

x⁴/4! f^iv (0) + x⁵/5! f^v (0) + x⁶/6! f^vi  (0)+ x⁷/7! f^vii (0)

f(x)=0 + 2x+x²/2! (0)+x³/3! (-8) + x⁴/4! (0)+ x⁵/5! (32)+ x⁶/6! (0)+ x⁷/7! (-128)
Using the Maclaurin’s series Equation you’ll arive at;
f(x)=2x – [(8x³)/(1×2×3)] + [(32x⁵)/(1×2×3×4×5)] – (128x⁷)/(1×2×3×4×5×6×7)

f(x)=2x – (4x²)/3 + (4x⁵)/15 – (8x⁷)/315

Question 2

a. Verify the convergence or otherwise of the given GP
2 + 6 +18 + 54 +…..
b. Given that A = 3y²zi -2x²yj- xyz²k   find the curl of A at (1,-2,1)

Solution

a. Applying the formular of GP

S_n=(a(1 – rⁿ))/(1-r)    r<1    S_n=(a(1 – rⁿ))/(r – 1)   r>1
S_n=(2(1-3ⁿ))/(3-1) = (2(1-3ⁿ))/2= (1-3ⁿ)
S_n=(1-3ⁿ )       n→∞
S_n=1 – 3^∞=1- ∞ = -∞
The series is a divergence series. As n tends to infinity 3ⁿ will become a very large number making the series Divergence

b. Note The curl of a function is always a vector quantity

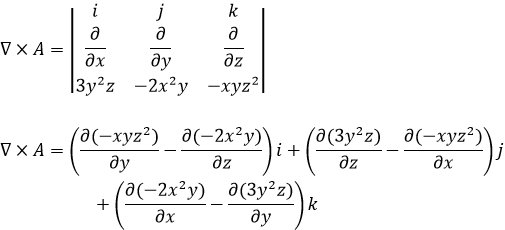= -xz²i +(3y² +xz²)j + (-4xy -6yz)k
at A(1,-2,1)
= -(1)(1)²i + (3(-2)² + 1(1)²)j + (-4(1)(2) -6(-2)(1))
The curl of A = -i +13j +k

Question 3

Evaluate
∬_sA ̅.n ̅ds,    where A ̅=18zi-12j+3yk 

S is the part of the plane 2x + 3y + 6z =12 Given that the projected surface S of A is in the plane xy and the projection points to z-axis direction

Solution

The formula for surface integral :

∬A.n ̅ds         A=18zi-12j+3yk
S : 2x+3yz+6z=12    x-  y plane  z-axis direction
∬A ̅  n ̂ds     n ̂=∇f/|∇f|     ds=dxdy/|n.k|
∬F n ̂ dxdy/|n.k|

f=2x+3y+6z-12
∇f=∇(2x+3y+6z-12)=2i+3j+6k
|∇f|=√(2²+3² +6² ) =√49 =7
Therefore we have;
n ̂=∇f/|∇f| = (2i+3j+6k)/7    

n.k=1/7(2i+3j+6k)
n.k = 1/7×6 = 6/7
A.n ̂ = (18zi-12j+3yk) . (1/7 (2i+3j+6k))
=(36z-36+18y)/7

From the equation of the surface (z axis direction)
z=(12-2x-3y)/6

Substituting z in the above equation becomes;
A.n ̂=1/7 (36(12-2x-3y)/6  – 36 + 18)
=1/7 (72 – 12x – 18y – 36 + 18y)
=1/7 (36-12x)
∬Fn ̅ds =∬1/7 (36-12x)  dxdy/6 ×7   remember n.k=7/6
∬6(6-12x)  dxdy/6
∬(6-12x)dxdy

To find the limit of the integration, take the x-y plane at which z=0 so that you can have:  2x+3y =12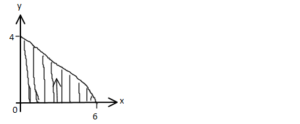
From the equation at x=0   y=4
From the equation at y=0   x=6
X varies from x=0  to x=6
Y varies from  y=0 t0 y = (12-2x)/3

∫₀⁶∫₀^((12-2x)/3) (6-2x)dxdy
∫₀⁶(6-2x)dx     (y)  ((12-2x)/2) ¦ 0
∫₀⁶(6-2x)dx ((12-2x)/2)
∫₀⁶(24-12x+4/3 x² )dx=24

 Question 4

a. Given that w = z²  + 4  determine   dw/dz at the point (2,3).
b. given that z₁=1 + j2,    z₂ = 4 – j3,   z₃ = -2 +j3  and   z₄ =  -5 -j      find.
i. z₁ + z₂ – z₃ in polar form
ii. z₁ z₂ z₃in exponential form
iii.   (z₁ + z₃) /(z₂ +z4) in cartesian form

Solution

a.
z = x+ iy
z² = (x+iy)² = x²+ 2xyi – y²
w = x²+ 2xyi – y² +4
w = x²– y² +4+ 2xyi
w= u +iv
u = x²– y² +4     v = 2xy
Differentiating u and v with respect to both x and y;

∂u/∂x=2x         ∂u/∂y=-2y.
∂v/∂x=2y         ∂v/∂y=2x
∂w/∂z = ∂u/∂x + j∂v/∂x  = ∂v/∂y –j ∂u/∂y
=2x+j2y = 2x – j(-2y)= 2x + j2y

Thus w = 2x + j2y

b.
z₁=1 + j2,    z₂ = 4 – j3,   z₃ = -2 +j3  and   z₄ =  -5 -j  

i. in polar (r, θ)
z₁ +z₂ +z₃ = (1 + j2) + (4 – j3) – ( -2 +j3 )
=(1+4+2) +j(2-3-3)
=7 –j4

r=√(7²+4² )=√65
θ=tan^-1(-4/7)= -29.7 ≈-30^o
-4 and 7 is on the 4^th quadrant
θ=360 – 30=330^o

     (√65  , 330^o)

ii. in exponentail Z = re^jθ
z₁ z₂ z₃= (1+j2)(4-j4)(-2+j3)
=(4-j3+8j+6) (-2+j3)
=(4+j5+6) (-2+j3)
=(10+j5) (-2+j3)
=-20 +j30-j10-15
=-35 +j20

r=√((-35)²+(20)² )=√1625 = 40.3

θ=tan^-1(20/-35)= -29.7≈ 30^o
θ=180 – 30= 150^o
z=40e^j150
Z = 40e^j150
Thus  z₁ z₂ z₃ in exponetial form is equal= 40e^j150

^iii.
(z₁+z₂)/(z₂-z₄ ) = [(1+j2)+(-2+j3)]/[(4-j3)—(-5-j) ]=[(-1+j5))/((9-j2) ]
Multiplying by the conjugate of  (9-j2)
=[(-1+j5)/(9-j2) ] × [(9+j2)/(9+j2)]
= (-9-j2+j40-10)/(9²+4)
=(9+j30-10)/(81+4) = (-1+j30)/85=-1/85 + j 30/85

=(-1/85 + j 30/85)

Question 6

a. using  De’alambert ratio test prove on the convergence or  otherwise of the series below

1 + 1/3 + 1/9 + 1/27 + 1/81 + …….

b. find (1+i)⁸ using Demoiver’s theorem

Solution

a.

D’alembert ratio test

k=U_(n+1) /U_n
k<1 convergent
k>1 divergent

1/3^o +1/3¹ +1/3² +1/3³ +1/3⁴

Therefore U_n=1/3ⁿ             U_(n+1) =1/3⁽ⁿ⁺¹⁾
Applying the D’Alembert formula
K=1/3⁽ⁿ⁺¹⁾ ÷1/3ⁿ
=1/3⁽ⁿ⁺¹⁾  × 3ⁿ/1= 3ⁿ/3⁽ⁿ⁺¹⁾

Applying law of indices
=3^{(n-(n+1)) =} 3^(-1)
k=1/3    the series is convergent since k<1

b.

Applying Demoiver’s Theorem:

(1+i)⁸     a=1   b=1  n = 8
Zⁿ=rⁿ (cosnθ + sinnθ )
r=√(a²+b² )   = √(1²+1² )=√2
θ=tan^-1(1/1) =45° = π/4\
Z = (√2)(cosn(π/4)+sinn(π/4))

Substituting the value of n = 8
Z⁸ = (√2 )⁸ (cos8(π/4)+sin8(π/4))
Z⁸=16(cos2π + sin2π )
cos2π = -1    and  sin2π = 0
Z⁸ = 16( -1 + 0 ) =-16
Therefor:  Z⁸ = -16

Question 7

Find the Fourier expansion  to represent

f(x)= π – x  for 0<x<2π

Solution

Using the formula of Fourier Series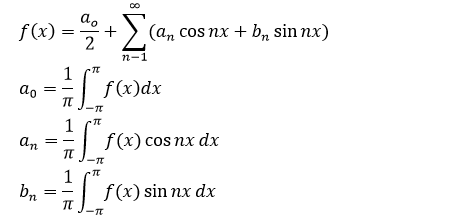
Finding the value of a_o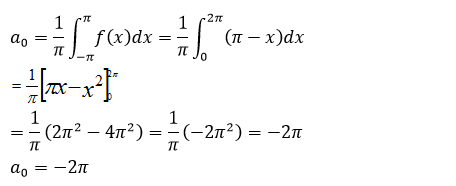
Now finding the value of a_n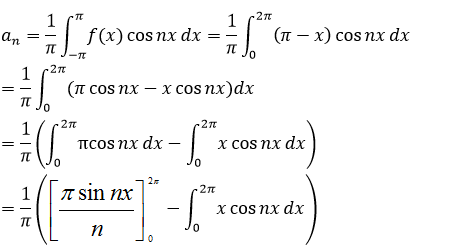Applying integration by part;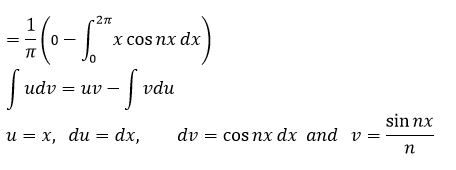
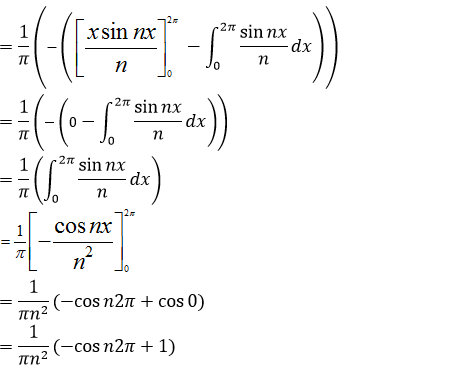
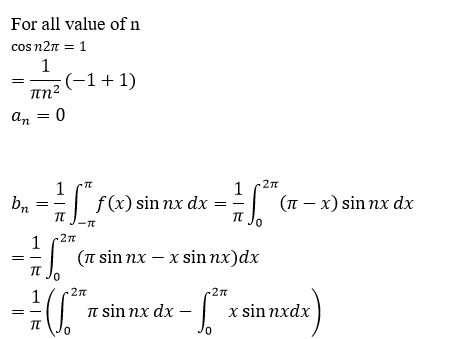
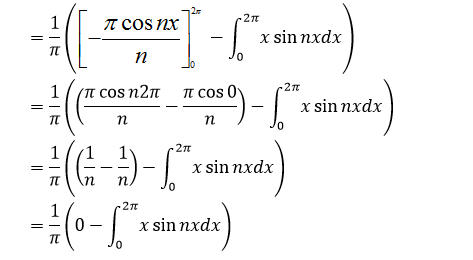
Apply integration by part;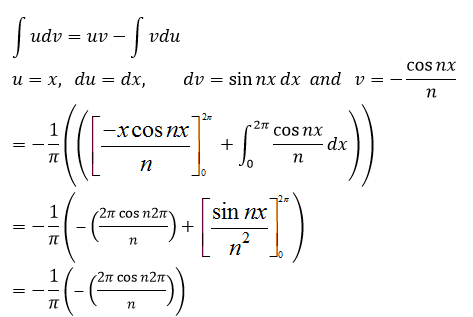

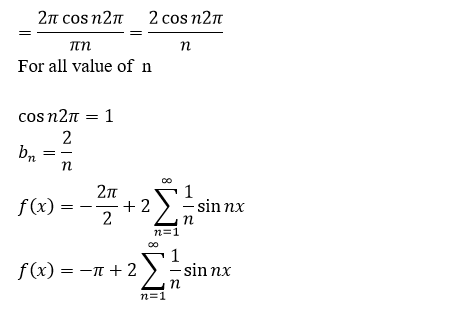
Question8

a. Evaluate the following if
Z₁ = 1 – j3,  Z₂ = -2 + j5  and  Z₃ = -3 –j4
i) Z₁Z₂ in (a + jb)
ii) form Z₁/Z₃ in polar form
iii) Z₁Z₂/ (Z1 +Z2)

b) Find Z₁Z₂Z₃

Solution

a)
i)  Z₁Z₂  = (1-j3) (-2 + j5)
= -2 +j5 +j6  -j²15
=-2 +j5 +j6 + 15
     Z₁Z₂ = 13 +j11

ii) Z₁/Z₃ = (1-j3)/(-3-j4)
Multiplying through by the conjugate of ( -3 + j4)
= (1-j3)/(-3-j4)  ×  (-3+j4)/(-3+j4)
= (-3+ j4+j9-j²12)/(3²+4² )
=9/25 + j13/25
=0.36 + j 0.52

Polar form (r,θ)  r=√(x²+y²)    θ = tan^-1(y/x)
r=√(0.36²+ 0.52² )   = √0.4 = 0.6
θ=tan^-1(0.52/0.36) = 60°
Z₁/Z₃ = (0.6, 60°)

ii) Z₁ + Z₂ = (1-j3) + (-2+j5)
= (1-2) + j(-3 +5)
= -1 +2j
Z₁ + Z₂ = -1 +2j       Z₁Z₂ =13 + j11

(Z₁ Z₂)/(Z₁+Z₂ ) = (13 + j11)/(-1+2)  ×  (-1-2)/(-1-2)
(-13-j26-j11-j² 22)/(-1²+2²)
=(9-j37)/5 = 9/5 –  j 37/5
= 1.8 – j7.4

Z = (x + jy)   ( Complex form)
Z = ( r, θ)     ( Polar form)
Z = re^-jθ       (Exponential form)

r=√((1.8)²+(7.4)² )   =√25.33 = 5.03
θ=tan^-1(7.4/1.8) = 76.3°
Z=5e^-j76.33

Question 9

a.   A = 3x²y – 2xyzj + yxk  Find
∇× A̅   at (1,-1,1)

b. Verify the convergence or otherwise of the GP      below
1+ 1/3 +1/9 + 1/27 +1/81 +⋯

Solution

a)  Finding the Curl of the vector

= ( z – 2xy)i + (0 – 0)j + (2yz -3x²)z
= ( z – 2xy)i + (2yz -3x²)z
At (1, -1, 1)
=(1 -2(1)(-1))i + (2(-1) (1) – 3 (1)²)z
=(1+2)i + (-2-3)z
=3i – 5z

b)  a=1,   r = 1/3÷1 = 1/3×1 = 1/3

S_n = (a(1 – rⁿ))/(1-r)
S_n = 1(1-(1/3)ⁿ ) / (1- 1/3)
S_n=((1- (1/3)ⁿ )) / (2/3)
S_n = (1- (1/3)ⁿ ) ÷  2/3
S_n= (1 – (1/3)ⁿ ) × 3/2
as  n→∞       (1/3)ⁿ= 0
S_n=(1-0) x 3/2 = 2/3
S_n=3/2      Therefore it is Convergence

Question 10

a) Expand  f(x) = e^7x using Maclaurin’s series expansion
b) Find    ∇∅= 1/|r|    where  r = xi + yj + zk

Solution

a)

f(x)= e^7x            f(0)= e⁰=1
fⁱ(x)= 7e^7x         fⁱ(0)= 7e⁰=7
fⁱⁱ(x)= 47e^7x      fⁱⁱ(0)= 47e⁰=47
fⁱⁱⁱ(x)= 343e^7x    fⁱⁱⁱ(0)= 343e⁰=343
f^iv(x)= 2401e^7x  f^iv(0)= 2401e⁰=2401
f^v(x)= 16807e^7x f^v(0)= 16807e⁰=16807

f(x)=f(0) + xf’’ (0) + x²/2! f’’(0) + x³/3! f’’’(0)+⋯
f(x)=1 + (x × 7) + (x²/2!  × 49) + (x³/3! × 343) + (x⁴/4!  × 2401) + (x⁵/5!  × 16807)
f(x)=1 + 7x + (49x²)/2 + (343x³ )/6 +(2401x⁴)/24 + (16807x⁵)/120

b)

r ̅= xi + yj + zk
|r ̅ |=√((xi)²+(yj)²+(zk)² ) = √(x² + y²+z² )
|r ̅ |=(x²+y²+z² )^1/2

∅=1/| ̅r| =1/(x²+y²+z² )^1/2 =(x²+y²+z² )^-1/2

∇∅ = (d(x²+y²+z² )^-1/2/dx) i  + (d(x²+y²+z² )^-1/2/dy) j + (d(x²+y²+z² )^-1/2/dz) k ……(i)

Now to find   (d(x²+y²+z² )^-1/2/dx)
let s =(x²+y²+z² )^-1/2  and  u =  x²+y²+z²
du/dx = 2x     du/dy = 2y      du/dz = 2z
s = u^-1/2
ds/du=-1/2 u^-3/2
ds/dx = ds/du × du/dx  = -1/2 u^-3/2  × 2x  = -x u^-3/2

Therefore (d(x²+y²+z² )^-1/2/dx) = ds/du × du/dx
= -x u^-3/2
Inserting the value of u = x²+y²+z²
(d(x²+y²+z² )^-1/2/dx)  = -x (x²+y²+z² ) ^-3/2 …………………….(ii)

Applying the same approach to (d(x²+y²+z² )^-1/2/dy)
ds/dy = ds/du × du/dy  = -1/2 u^-3/2  × 2y  = -y u^-3/2
Thus (d(x²+y²+z² )^-1/2/dy)  = -y (x²+y²+z² ) ^-3/2  …………..(iii)

Also (d(x²+y²+z² )^-1/2/dz) = -1/2 u^-3/2  × 2z  = -z u^-3/2
(d(x²+y²+z² )^-1/2/dz)  = -z (x²+y²+z² ) ^-3/2 …………………….(iv)

Inserting equation (i), (ii), (iii) and (iv)  in equation (i)
∇∅= -x (x²+y²+z² ) ^-3/2 i -y (x²+y²+z² ) ^-3/2 j -z (x²+y²+z² ) ^-3/2  k
∇∅= – (x²+y²+z² ) ^-3/2 (xi + yj+ z)

Question 11

a) Expand  f(x) = In(x-2)  as a series of ascending power of x

b) If  F =6xyi + y² j   Evaluate  ∫_c Fdr    for C at (0,0)  to (1,2)
Where C is the curve in the xy plane define by y = 2x

Solution

a) f(x)=f(0) + xf’’ (0) + x²/2! f’’(0) + x³/3! f’’’(0)+⋯

f(x)=In(x-2)           f(0)=In(-2)
f’(x)=1/(x-2)          f’(0)=-1/2
f’’(x)=(-1)/(x-2)²    f’’(0)=-1/4
f’’’(x) = 2/ (x-2)³    f’’’(0)=-1/4
f^iv (x)= -6/(x-2)⁴     f^iv (0)=-3/8
f^v (x)=24/(x-2)⁵      f^v (0)=-3/4

b)

w= ∫_c Fdr          r ̅ = xi+yj      dr  ̅ =dxi + dyj
∫(6xyi+y² j)(dxi + dyj)…….(i)

y=2x      dy/dx=2     dy=2dx
Inserting the value of y and dy in equation (i)
∫(6x(2x)dx + (2x)² . 2dx)
∫(12x² dx + 8x² dx)
∫20x² dx

C at (0,0)  to (1,2)  Using the limit of x 0 to 1
∫₀¹20x² dx
=(-20x³/3) limit of 0 to 1
=(20(1)³)/3)=20/3
w= =20/3

Question 12

a)  Give the w = (3z – j)² determine  dw/dz  at the point  (2,3)
b) Does the series 2/3 + ¾ + 4/5 +5/6 + ….. converge or diverge

Solution

a)
dw/dz    = du/dx + j dv/dx    =  dv/dy- j du/dy
du/dx + j dv/dx    =  dv/dy- j du/dy
Thus du/dx = dv/dy   and dv/dy  = -du/dy

W= (3z – j)² = (3z – j) (3z – j)
W = 9z2 –j 3z –j3z + j2
W = 9z² –j6z -1……. (i)

Recall z = x+ jy
Z²= (x + jy)(x+ jy) = x² + j2xy – y2
Substituting the value of z and z²  in eqn (i)

W = 9(x² + j2xy – y2) – j6(x + jy) – 1
W = 9x² + j18xy –9 y2 – j6x + 6y -1
W = (9x² –9 y² + 6y -1) + j(18xy– 6x)

Note that W = u + jv  Therefore;
u = 9x² –9 y² + 6y -1    and v = 18xy – 6x

du/dx = 18x             du/dy = -18y + 6
dv/dx = 18y – 6       dv/dy = 18x
Using the formula   du/dx + j dv/dx = dv/dy – j du/dy   
= 18x + j(18y – 6) =18x – j(-18y + 6)
= 18x +j(18y -6) = 18x + j(18y -6)
dw/dz = 18x + j(18y -6)

dw/dz at (2, 3)
dw/dz = 18(2) + j(18(3) – 6)
dw/dz = 36 +j48

b) Finding the equation of the series 2/3 + ¾ + 4/5 +5/6 + …..
 we get: S_n=(n+1)/(n+2)
limn→∞    S_n=(∞+1)/(∞+2) = ∞/∞
S_n=undetermined
The series is divergence

Question 13

Find the Fourier series for the function shown. consider one cycle between x = -π and π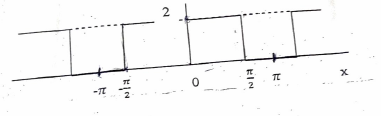

Solution

considering different integers for the value of n

If n is even

If n is odd but having the value of 1, 5, 9…..

If n is odd but having the value of 3, 7, 11…..