How many years older will you be 1.50 gigaseconds from now? (Assume a 365-day year)
a) 6 years b) 74 years c) 50 years d) 31.7 years
1.5G sec from now, assuming 365days = 1 year.
1.5 x 10⁹ sec = x years.
60 sec = 1min, 60 min = 1 hrs, 24 hrs = 1 day.
365 days = 1 year, N ow; using newtons unity bracket method;
1 year x (365days/ 1 year) x (24 hrs/ 1 day) x (60 min/ 1 hr) x (60 sec/ 1 min)
31.536 X 10⁶ sec = 1 year = 365 days
1.50 x 10⁹ sec = 1 years = x
X = 47.56 years. C
The equivalent of 5yd3 in cubic meters is:
a) 6m3 b) 4m3 c) 6.12m3 d) 3.82m3
5 yds equivalent in m³ = ?
1 yd = 0.9144m = ( 0.9144m)³
1 yd = 0.7646m³
5yds x ( 0.7646m³/ 1 yds ) = 3.8228 m³
Therefore 5 yds = 3.8228 m³ D
The most powerful engine available for the classic 1963 Chevrolet Corvette Sting Ray developed 360 horsepower and had a displacement of 327 cubic inches. This displacement in litres (L) by using only the conversions 1L = 1000cm3 and 1 in = 2.54cm is:
a) 6.1 b) 3.9 c) 5.4 d) 5.9
P = 360hp., x = 327 inch³
X in (L) = ?
Given : 1 L = 1000cm³ 1 in = 2.54 cm
x = 327 in³
327 in³ x ( 2.54 cm / 1 in )³ x 1 L/ 1000cm³
= 5.3586 L = 5.4 C
If s is the distance in metres and t the time in seconds, what must be the dimensions of a in the following equation? s = ½ at2
a) LT b) LT-1 c) L-2T d) LT-2
S = distance ( meter ) , t = Given ( sec ).
What is the dimension of a in
S = ( ½ )at² . the dimensions are ;
S = L , t = T
a = ( L/T² ) = LT̅²
all dimensions have to be the same
that is left hand side = right hand side.
Now : S = L
at² = ( L/ T² ) X T² = L
a = ( L/ T² ) = L T-2 D
Use dimensional analysis to determine which of the following equations is not correct.
a)ʎ = vt b) F = ma c) F = mv/t d) v = (2gt)1/2
a) ʎ = vt ; ʎ = L ; V = ( L/T ) , t =T
ʎ = Vt
L = L/T X T = L
b) F = ma ; F = N = ML. T-2
M = M , a = L T-2
Therefore F = ML T-2 = ML T-2
c) F = (mv/t) ; F = ML T-2 , m = M , t = T
V = LT-1
Therefore ML T-2 = M X L T-1 X T-1 = M X L T-2
d)V = (2gt) 1/2 ; V = L T-1 , t = T,
g = L T-2
L T-1 = 2(L T-2 X T )1/2
L T-1 = 2(L T-1 ) = 2 L1/2 T-1/2
Therefore, L T-1 is not equal to 2 L1/2 T-1/2 D
Find the angle between the following pair of vectors: A = 3.00i + 5.00j and B = 10.00i + 6.00j
a)180 b) 200 c) 280 d) 300
A = 3.00i + 5.00j and B = 10.00i + 6.00j
Using dot product
A.B = /A/ /B/ cos θ
A.B = (3i + 5j) . (10i + 6j)
= 3(10) + 5(6)
= 30 + 30 = 60 units
/A/ = √ (√ 32 + 52)
= √ (9 + 25) = √ 34.
/B/ = √102 + 62
= √ (100 + 36) = √ 136.
cos θ = A.B / (/A/ /B/) = 60 / (√ 34 x √ 136)
= 0.88235
θ = cos-1 0.88235
= 28.07ᵒ
= 28
The vector sum A + B from question above is:
a) 7i – j b) 13i + 11j c) 13i -11j d) 11i +13j
A̅ + B̅ = ?
Since A̅ = 3i + 5j and B̅ = 10i + 6j
A̅ + B̅ = ( 3i + 5j ) + ( 10i + 6j )
A̅ + B̅ = ( 3i + 10j ) + ( 5i + 6j ) = 13i + 11j
B
A car travels in the x-direction on a straight and level road. For the first 4.00 seconds of its motion, the average velocity of the car vax = 6.25m/s. how far does the car travel in 4.00 seconds?
a) 20m b) 250m c) 50m d) 25m
T = 4.00 sec, velocity = 6.25m/s , s = ? , t = 4sec
Now velocity = ( distance/ time ) = distance = velocity x time
S = V X T = 6.25 x 4 = 25m D
Use the following information to answer questions the next 3 questions. A major leaguer hits a baseball so that it leaves the bat at the speed of 30.0m/s and at an angle of 36.90 above the horizontal. You can ignore air resistance.
The maximum height reached by the baseball is:
a)16.5m b) 0.92m c) 21m d) 17.5m
Maximum height ( H ) = U2sin2 ᴓ/2g
Given ; U = 30m/s , ᴓ = 36.9ᵒ
= (( 30 )2 x ( sin 36.9 )2/ (2 x 9.8 )) = 16.53m A
The total time of flight is:
a) 3 s b) 2.9 s c)3.7 s d) 4.1 s
Time of flight (t) = Usin ᴓ/ g and the total time of flight (T) = 2t =2Usin ᴓ/g= 2 x 30 x sin ( 36.9 )/9.81 = 3.67 = 3.7s C
What are the magnitude and direction of the baseball’s velocity when it returns to the level at which it left the bat?
a)36.9 m/s, 30.00 b) 30.0 m/s, 36.90 c) 30.0 m/s, 36.90 above the horizontal d) 30.0 m/s, 36.90 below the horizontal
Since for the entire trajectory, the projectile was unaffected by external factors. Velocity = constant and ᴓ = constant above the horizontal = V = 30mls, ᴓ = 36.9ᵒ above the horizontal C
Σ F = ma is the mathematical expression of:
a)Newton’s first law b) Newton’s second law c) Newton’s third law d) Law of conservation of momentum
Newton’s second law states; the rate of change of momentum is directly proportional to the applied force, and takes place in the applied force and takes place in the direction in which the force acts.
F α( MV – MU) / G = m ( v – u )/ G
F = ma = F = Kma where k = constant B
A branch of physics that deals with the relationship of motion with the forces that cause it is called:
a)Dynamics b) Statics c) Kinematics d) None of the above
Dynamics is the branch of physics or study of bodies in motion with the forces associated with them. A
An object of mass 4kg moves around a circle of radius 100cm with a constant speed of 30m/s. how much time does it take the object to make one revolution?
a)2 s b) 0.02 s c) 0.21 s d) 0.03 s
m = 4 kg, r = 100cm = 1m.
speed = 30m/s , t = ?
for one revolution, the time taken is the period (T) = 2π /ω.
ω = V/r = 30/1 = 30rad/sec
T = 2π /30 = 0.2094 = 0.21sec C
A boy having a mass of 75kg holds in his hands a bag of rice weighing 40N. With what force does the floor push up his feet?
a)115N b) 736Ns c) 750N d) 776N
mb = mass of boy
W = weight of rice = 40 N
From newton’s third law ; “ force of action and reaction are equal and opposite “
Let RE = force of reaction by the floor.
W = 40N , Wh = weight of boy = mg
Wb = 75 x 9.81 = 735.75 N
Therefore RF = Wb + Wr = 735.75 + 40 = 775.75N.
R = 775.75 = 776N D
A passenger walks with a velocity of 1m/s in a train that is moving with a velocity of 3m/s. if the passenger moves in the direction at which the train is moving, at which velocity does a person standing beside the train see the walking passenger moving?
a) 3m/s b) 2m/s c) 4m/s d) 5m/s
Velocity of passenger = Vp = 1 m/s.
velocity of train = Vt = 3m/s
Train and passenger are moving in the same direction with different velocities. Therefore, for a person standing with new velocity, will see the person walking as follows;
The person standing has velocity = Vt = 3m/s
The person standing is the reference point / observer.
Therefore the relative velocity of the standing person and the walking person on the same direction = 3 – 1 = 2m/s B
A 68.5-kg skater moving initially at 2.4m/s on rough horizontal ice comes to rest uniformly in 3.52 seconds due to friction from the ice. What force does the friction exert on the skater?
a)46.7N b) 672N c) 458N d) 164.4N
m = 68.5kg , u = 2.4m/s , v = 0, t = 3.52s
F = force due to friction = ?
F = ma = a = V – U / t = 0 – 2.4 / 3.52 =
F = 68.5 x ( 0.6818) = – 46.7N
-ve since the force is retarding
F = 46.7N A
Use the following information to answer questions the next two question
At the surface of Jupiter’s moon Io, the acceleration due to gravity is g = 1.81ms-2. A watermelon weighs 44.0N on the surface of the Earth.
What is the watermelon’s mass on Earth?
a)44.0kg b) 4.49kg c) 24.3kg d) 8.13 kg
At jupiter’s moon, g = 1.81m/s2
At Earth surface, g = 9.81 m/s2
Let W = weight of watermelon at the Earth’s surface .
W = mg = m x 9.81 @ Earth
M = W/ 9.81 = 44/9.81 = 4.485kg
m = 4.485kg = 4.49kg B
What are the watermelon’s mass and weight on the surface of Io?
a)44.0 kg, 8.13N b) 4.49kg, 44.0N c) 24.3kg, 8.13N d) 4.49 kg, 8.13N
Water melon’s mass and weight on surface of io, Jupiter moon are Mj and Wj are unknown.
Now, we known that weight of an object varies with force of gravity while the mass of an object Is a constant parameter at all points.
Therefore; Me = Mj = 4.49kg.
Wj = Mj x Gj = 4.49 x 1.81
Wj = 8.1269 = 8.13N
Therefore the mass and weight of the water melon on the surface of is respectively are 4.49kg and 8.13 D
A man pushes on a piano with mass 180kg so that it slides at constant velocity down a ramp that is inclined at 11.00 above the horizontal floor. Neglecting any friction acting on the piano.

The magnitude of the force applied by the man if he pushes parallel to the incline is:
a)176.7N b) 337N c) 343N d) 300N
m = 180 kg , g = 9.81m/s2
ᴓ = 11.0ᵒ , F = ? , W = mg
if the man pushes the block parallel to the inch = F = Wsin ᴓ
F = ( 180 x 9.81 ) sin ( 11ᵒ ) = 336.93N
F = 337N B
How many joules of energy does a 100-watt light bulb use per hour?
a)0.36 MJ b) 36 MJ c) 1.67 MJ d) 6 kJ
Power = 100W = 100j/s
Time = 1hr = 3600 sec
Power = work done / time = energy / time .
Work done = power x time = 100 x 3600
Work done = 360000 = 0.36MJ A
How fast would a 70-kg person have to run to have 360 kJ of energy?
a)111m/s b) 10.3m/s c) 90m/s d) 101m/s
m = 70kg, energy = 360KJ
Speed = V = ?
K.E = 1/2 MV2 = V2 = K.E X 2 / M
V2 = 3600 x 103 x 2 / 70 = V = 101m/s D
Use fig.1 to answer the next three (3) questions
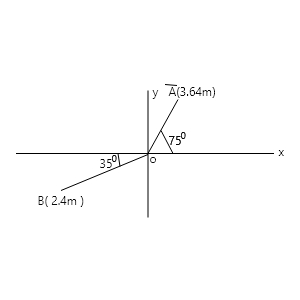
The vector in terms of the unit vectors i and j is:
a)0.93i – 3.50j b) 0.7i + 3.50j c) 3.50i +0.93j d) 0.93i + 3.50j
X = Acosᴓi = -2.4cos35i = -1.97i
Y = Asinᴓij = 3.6sin75j = 3.4773j
Therefore A̅ = Acosᴓi + Asinᴓj = 0.93i + 3.5j
D
The vector B in terms of the unit vectors i and j is:
a)1.97i – 3.50j b) -1.97i – 1.38j c) 1.97i + 1.38j d) 1.97i – 1.38j
X = -Bcosᴓi = -2.4cos35i = -1.97i
Y = -Bsinᴓj = -2.4sin35ᴓj = -1.38j
Therefore B̅ = Bcosᴓi + Bsinᴓj = -1.97i – 1.38j
B therefore both x and y are –ve!
The vector C = A – B from fig 1 is:
a)2.90i – 4.88j b) 2.90i + 4.88j c) -2.90i – 4.88j d) -2.90 + 4.88j
C̅ = A̅. B̅
Since A̅ = 0.93i + 3.5j and
B̅ = -1.97i – 1.38j
C̅ = ( 0.93i + 3.5j ) – ( -1.97j – 1.38j )
C̅ = ( 0.93i + 1.97j ) + ( 3.5j + 1.38j )
C̅ = 2.9i + 4.88j B
The graph in fig. 2 shows the velocity of a motorcycle police officer plotted as a function of time. Use fig. 2 to answer the next two (2) questions
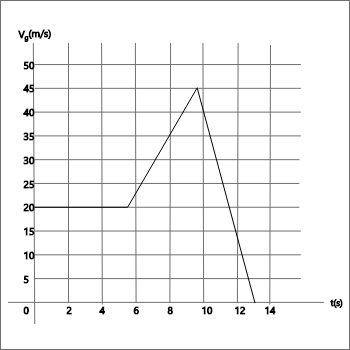
The instantaneous acceleration at t = 3 seconds is:
a)60ms-2 b) 20 ms-2 c) 0 ms-2 d) 3 ms-2
Now ; acceleration = (change in velocity )/ time
From the given graph, V = constant
Therefore the acceleration is zero for constant velocity = acceleration
a = 0m/s2 C
How far does the officer go in the first 5 seconds?
a)100m b) 20m c) 50m d) 1000m
Distance = velocity x time = 20 x 5 = 100m A
Use the following information to answer the next three (3) questions
A 6-kg toy cart undergoes acceleration in a straight line (the x-axis). The graph in fig.3 shows this acceleration as a function of time.
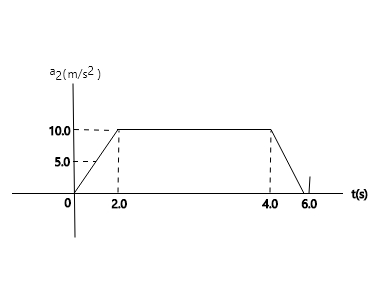
The maximum net force on this part is:
a) 44.1N b) 5.0N c) 90N d) 45N
Fmax + Fmin = ƩF = Fnet = m ( a1 + a2 )
= 6 ( 10 + 5 ) = 90N C
During what time is the net force on the cart a constant?
a) 0.0s to 6.0s b) 0.0s to 4.0s c) 2.0s to 4.0s d) 2.0s to 6.0s
The net force is constants throughout the whole motion because its includes both max and min
A
When is the net force equal to zero?
a) 0.0s only b) 0.0s and 6.0s c) 6.0s only d) 2.0s and 4.0s
Net force would be zero when there is no acceleration .
The Fnet = amax + amin = 0 , t = 0 sec A
If you like our tutorials you can subscribe to our YouTube channel here
Disclaimer
This entire solution may not be 100% accurate, any mistake or typo found should be reported to SmartBukites Management through the following email [email protected] »
All the custom solutions are written for individual research and reference ONLY. SmartBukites does not promote plagiarism in any form and firmly believes that Student will use the solutions models in their individual efforts.
Related Courses
- Electricity & Magnetism
- Elementary Mathematics I
- Probability I
- Behaviour Of Matter
- Elementary Mathematics Calculus
Do you have a Question to Ask?
SmartBukites have a Facebook Group which allows everyone to ask, answer and seek academic help. At SmartBukites, we believe Smart approach to Education will go along way in easing human academic struggle.
Click the link to join now!!! https://web.facebook.com/groups/675122219621351
