Computer Engineering Questions and Solution

Question 1

What are combinational circuits?

b. What are the different types of combinational logic circuits? Draw table for 4 types or different logic gates

c. A certain system contain two identical circuits operating in parallel. As long as both are operating properly, the output of both circuit are always the same. If one of the circuit fails, the outputs will be at opposite levels at some time. Decide a way to detect that a failure has occurred in one of the circuits.

Solution

a.  A combinational logic circuit:

This is a circuit that performs an operation assigned logically by a Boolean expression or truth table (i.e their outputs depends on only the present inputs).

b.   There are three types of combinational logic circuits:

• Arithmetic and combinational circuits – Adders, Subtractors, Multiplexers, Comparators.
• Data handling combinational circuits – Multiplexers, DE multiplexers, priority encoders, decoders.
• Code converting combinational circuits – Binary to Gray, Gray to Binary, Binary to Excess 3, Seven segment etc.

Types of combinational logic Gates and Truth table

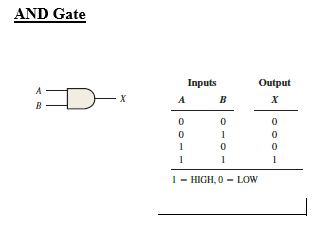
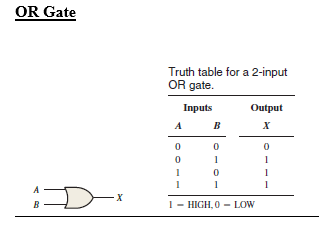
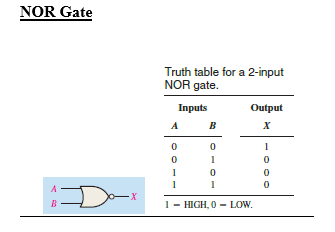
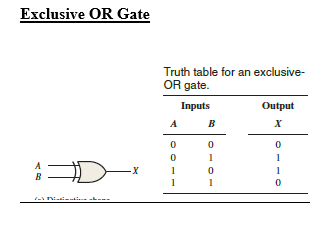
Thomas L. Floyd

c.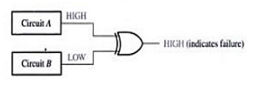 

• A failure in either one of the circuits produces differing outputs, which cause the XOR inputs to be at opposite levels.
• This condition produces a HIGH on the output of the XOR gate, indicating a failure in one of the circuits.

Question 2

• a)  As a computer engineer, describe how we can implement these applications
  • Seat belt alarm system
  • Intrusion detection system

• b) Verify the two laws of De Morgan’s theorems and show that they are equal by Illustrating it with truth tables

Solution

• a)
  • i)

An AND gate is used in a simple automobile seat belt alarm system to detect when the ignition switch is on and the seat belt is unbuckled.

If the ignition switch is on, a HIGH is produced on input A of the AND gate. If the seat belt is not properly buckled, a HIGH is produced on input B of the AND gate. Also, when the ignition switch is turned on, a timer is started that produces a HIGH on input C for 30 s.
If all three conditions exist—that is, if the ignition is on and the seat belt is unbuckled and the timer is running—the output of the AND gate is HIGH, and an audible alarm is energized to remind the driver.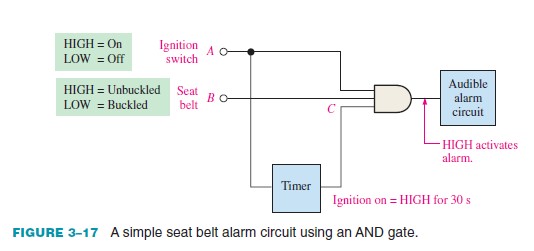

Thomas L. Floyd

• ii)
  This system is used for one room in a home-a room with two windows and a door.

The sensors are magnetic switches that produce a HIGH output when open and a LOW output when closed. As long as the windows and door are secured, the switches are closed and all three of the OR gate inputs are LOW.

When one of the windows or door is opened, a HIGH is produced on that input to the OR gate and gate output goes HIGH. It then activates and latches an alarm circuit to warn of the intrusion.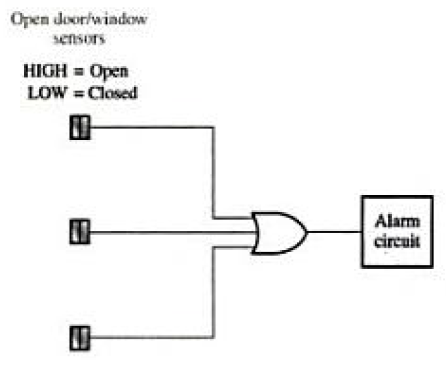

Intrusion detection system

• 2b)  The Morgan’s Theorems

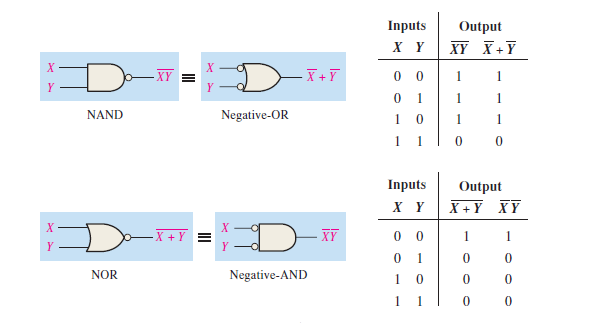
Thomas L. Floyd

Question 3

a.  Derive the Boolean expression and construct the switching circuit for column5 and column 6 o the truth table shown below

A	B	C	D	E	F
0	0	0	1	1	1
0	0	1	1	0	0
0	1	0	0	0	1
0	1	1	0	1	0
1	0	0	0	1	1
1	0	1	0	0	1
1	1	0	1	0	0
1	1	1	0	0	0

• b. Simplify the following using Boolean algebra simplification
  • F̅ . G̅. H + F̅.G.H + F.G̅.H
  • R(P.Q + P.Q̅) + R̅(P̅.Q̅  + P̅.Q)

Solution

• a)

A	B	C	D	E	F
0	0	0	1	1	1
0	0	1	1	0	0
0	1	0	0	0	1
0	1	1	0	1	0
1	0	0	0	1	1
1	0	1	0	0	1
1	1	0	1	0	0
1	1	1	0	0	0

Bringing the SOP of each Column

• The Column 4 (D) 000, 001 and 110
  D = A̅ B̅ C̅ + A̅ B̅ C + ABC̅

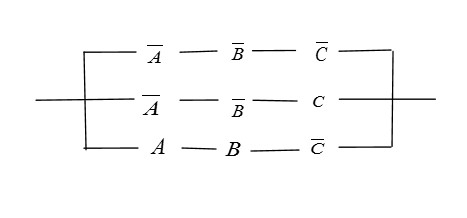
• The Column 5(E) 000,   011 and 100
  E = A̅ B̅ C̅ + A̅BC + A B̅ C̅

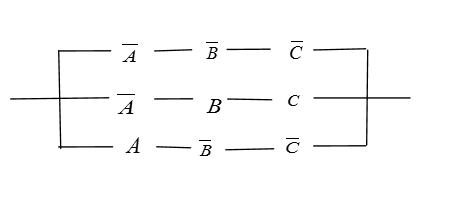
• The Column 6 (F)
  000,  010,  100  and 101
  E = A̅ B̅ C̅  + A̅BC̅ + A B̅ C̅ + AB̅C

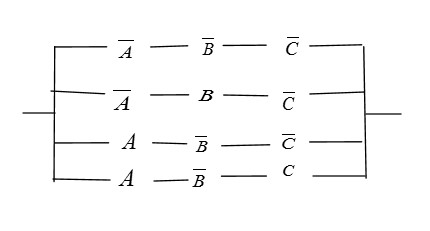
• b)
  • i) F̅ G̅ H + F̅ G H + F G̅ H
    F̅H(G̅ + G) + F G̅ H
    F̅H(1) + FG̅H
    H(F̅ +FG)   but F + FG̅ = F̅ + G̅
    H(F̅ + G̅)
    HF̅ + HG̅
    
    K – Map reduction can also be used in verifying if the answer is correct with 001, 011 and 101 from the equation
  • ii) R(PQ + PQ̅) + R̅(P̅Q̅ + P̅Q)
    RPQ + RPQ̅ + R̅ P̅ Q̅ + R̅ P̅ Q
    RP(Q+ Q̅) + R̅ P̅ (Q̅ + Q)
    RP(1) + R̅ P̅(1)
    RP + R̅ P̅
    
    K – Map reduction can also be used in verifying if the answer is correct with 111, 101, 000 and 010 from the equation

Question 4

• a) Write 4 rules for karnaugh map implementation

• b) Use Karnaugh map techniques to simplify the following Boolean expression
  • P̅ Q̅ R̅ + P Q R̅ + P Q̅ R
  • A̅ B̅ C̅ D + A̅ B̅ C D̅ + A B̅ C D̅

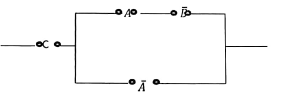
• c) Determine the Boolean expression and construct a truth table for the switching circuit shown below

Solution

a.Rules of K- Map

• Groups may not include any cell containing a zero.
• Groups must contain 1,2,4,8 or evenly grouped members.
• Groups may overlap.
• Each group should be large as possible.

• b)
  
  • P̅ Q̅ R̅ + P Q R̅ + PQR + P Q̅ R
    P̅ Q̅ R̅ = 000     P Q R̅ =110    PQR = 111    P Q̅ R = 101

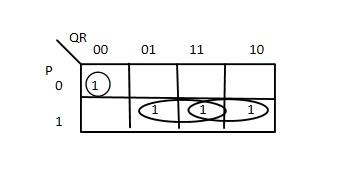
P̅ Q̅ R̅ + PR + PQ

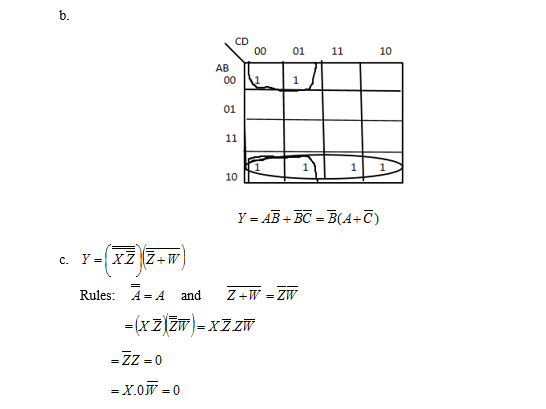
• A̅ B̅ C̅ D + A̅ B̅ C D̅ + A B̅ C D̅
  A̅ B̅ C̅ D = 0001     A̅ B̅ C D̅ =0010      A B̅ C D̅= 1010
  A̅ B̅ C̅ D + B̅CD̅

• c)

C(AB̅ + A̅) = AB̅C + A̅C

A	B	C	A̅	B̅	AB̅C	A̅C	AB̅C + A̅C
0	0	0	1	1	0	0	0
0	0	1	1	1	0	1	1
0	1	0	1	0	0	0	0
0	1	1	1	0	0	1	1
1	0	0	0	1	0	0	0
1	0	1	0	1	1	0	1
1	1	0	0	0	0	0	0
1	1	1	0	0	0	0	0

Question 5

• a) From the truth table below obtain the Sum of product(SOP) and Product of Sum (POS) .

A	B	C	D	E
0	0	0	0	1
0	0	0	1	1
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

• b) Draw the Karnaugh map and obtain the reduced Boolean expression

• c) Using De Morgans theorem and other Boolean algebra theorems to simplify the following

Expression: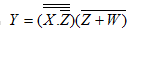

Solution

• a)

A	B	C	D	E
0	0	0	0	1
0	0	0	1	1
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

• The Sum of Product (SOP) = A̅ B̅ C̅ D̅ + A̅ B̅ C̅ D + A B̅ C̅ D̅ + A B̅ C D̅ + A B̅ C D
• The product of Sum(POS) = (A + B + C̅ + D)(A + B + C̅ + D̅)(A + B̅ + C + D) (A + B̅ + C + D̅)(A + B̅ + C̅ + D) (A + B̅ + C̅ + D̅)(A̅ + B̅ + C + D̅)(A̅ + B̅ + C̅ + D) (A̅ + B̅ + C̅ + D̅)

Question 6

• a) Standardize the following Boolean algebra
  • AB + A̅BD + A̅CD̅
  • (A + B + C + D̅)(A + B + C) (A + B̅ + C + D)
  • A̅BC + ABC̅ + ABC + AB

• b) Obtain the truth table for the following Boolean expression
  Y = A̅ + B̅C

• c) From the truth table obtain SOP and POS

Solution

• a)
  • AB + A̅BD + A̅CD̅
    (C + C̅) = 1     (B + B̅) =1    (D + D̅) =1
    AB(C + C̅) + A̅BD(C + C̅)  + A̅CD̅(B + B̅)
    ABC +ABC̅ + A̅BDC + A̅BDC̅ + A̅ C D̅ B + A̅ C D̅ B̅
    (D + D̅) = 1
    ABC(D + D̅)  +ABC̅(D + D̅)  + A̅BDC + A̅BDC̅ + A̅ C D̅ B + A̅ C D̅ B̅
    ABCD + ABCD̅  +ABC̅D + ABC̅ D̅  + A̅BDC + A̅BDC̅ + A̅ C D̅ B + A̅ C D̅ B̅
    Re-arrange the expression
    ABCD + ABCD̅  +ABC̅D + ABC̅ D̅  + A̅BCD + A̅B C̅ D+ A̅ B C D̅ + A̅ B̅ C D̅
  • (A + B + C + D̅) (A + B + C ) (A + B̅ + C + D)
    Add DD̅ = 0 to (A + B + C )
    (A + B + C + D̅) (A + B + C + (DD̅))   (A + B̅ + C + D)
    (A + B + C + D̅) (A + B + C + D)(A + B + C + D̅  ) (A + B̅ + C + D)
  • A̅BC + ABC̅ + ABC AB
    (C + C̅) = 1
    A̅BC + ABC̅ + ABC + AB(C + C̅)
    A̅BC + ABC̅ + ABC + ABC + ABC̅

• b) Y = A̅ + B̅C

A	B	C	A̅	B̅	B̅ C	Y = A̅ + B̅C
0	0	0	1	1	0	1
0	0	1	1	1	1	1
0	1	0	1	0	0	1
0	1	1	1	0	0	1
1	0	0	0	1	0	0
1	0	1	0	1	1	1
1	1	0	0	0	0	0
1	1	1	0	0	0	0

• c)
  • The SOP of the truth table = A̅ B̅ C̅ + A̅ B̅ C + A̅ B C̅ + A̅ B C + A B̅ C
  • The POS of the truth table = (A̅ + B + C) (A̅ + B̅ + C) (A̅ + B̅ + C̅)

Question 7

• a)  A car seat belt interlock requires the car should only start if the driver’s seat belt is fastened and either the front seat is unoccupied or the front passenger seat occupied and the passenger seat belt is fastened.
  • Obtain the truth table o the system
  • Obtain the SOP Boolean expression for the system
  • Use Karnuagh map to simplify the SOP Boolean expression
  • Implement the system using AND, NOT and OR logic gates

• b)  A bank vault has 3 locks with a key for each lock. Key A is owned by the bank manager.
  Key B is owned by the senior bank teller. Key C is owned by the trainee bank teller.
  In order to open the vault door at least two people must insert their keys into the assigned locks at the same time. The trainee bank teller can only open the vault when the bank manager is present in the opening.
  • Determine the truth table for such a digital locking system
  • Design, using Karnuagh Map techniques, a minimum AND-OR gate network to realize the locking system.

Solution

a. Assumptions:

A = Driver
B = Passenger seat occupied
C = Passenger Seat Belt
D = Car Start

Considering A, B, C and D the truth table will be;

When
A = 0( Driver seat belt OFF)  A = 1( Driver seat belt ON)
B = 0 ( Passenger seat Not Occupied) B = 1 ( Passenger seat Occupied)
C = 0 ( Passenger seat belt OFF)        C = 1 ( Passenger seat belt ON)
D = 0 (Start not Enable)      D = 1 ( Start Enable)

i.

A	B	C	D
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

Truth Table

• For 000, 001, 010 and 011 Since the driver seat BELT is OFF the Start will Not be ENABLED (0)
• For 100 The driver seat BELT is ON and  there is no passenger so the Start will be ENABLED (1)
• For 101 The driver seat BELT is ON, the passenger seat belt is ON without no passenger so the Start is ENABLED (1)
• For 110 The driver seat BELT is ON, the passenger seat is Occupied but the passenger Seat BELT is OFF, therefore the Start is Not ENABLED (0)
• For 111 everything is ON therefore the Start is ENABLED (1)

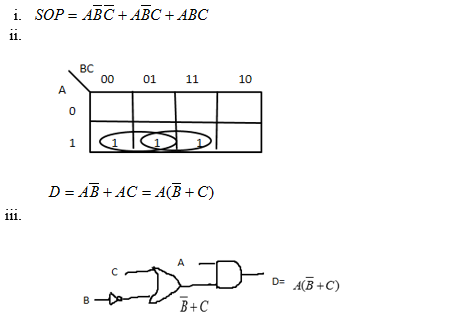
SOP, Reduce Boolean Expression and the Circuit Implementation

b.

Assumptions :

A = Bank manager
B = Senior bank teller
C = Trainee bank manager
Z= Door open

At least two people must be present. For the trainee the door can only be open when the bank manager is present.

A	B	C	Z
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Truth table

• 
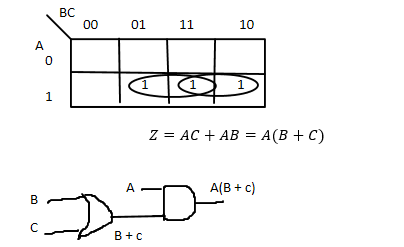
  K-Map and Network of the locking system.

Question 8

• a) A water tank feeds three separate processes. When any two of the processes are at the same time, a signal is required to start a pump to maintain the head of the water in the tank. Devise a logic circuit using Nor-gates only to give the required signal.

Solution

• a) The Boolean expression to meet the signal requirements is;
  Z = A(B + C) + B(A + C) + C(A + B)
       AB + AC + AB + BC + AC + BC
       AB + AB + BC + BC + AC + AC
       AB(1 + 1) + AC(1 + 1) + BC(1 + 1)
       AB + AC + BC
       A(B + C) + BC

Now implementing the circuit with a Nor-gate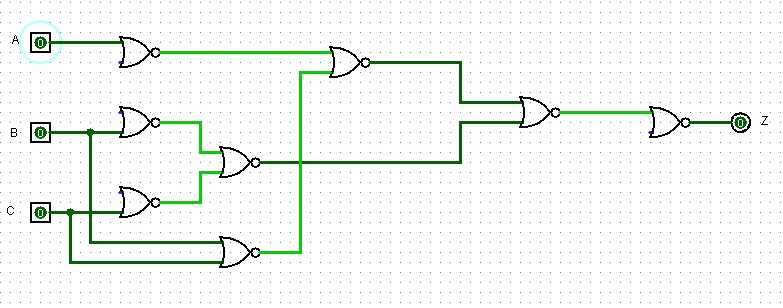

A logic circuit to satisfy the Boolean expression

Z = A. (B+C) + B.C

If you like this tutorial, subscribe to our YouTube channel here

Related Courses

• Engineering Mathematics III
• Electronics Engineering I »
• Circuit Theory I