a) Proof that
∫𝑋𝑛𝑑𝑥= 𝑋𝑛+1 /(𝑛 + 1) + 𝐶 𝑓𝑟𝑜𝑚 𝑑(𝑋𝑛)𝑑𝑥 = 𝑛𝑋𝑛−1
b)Evaluate
∫ (𝑥3−2𝑥2−4𝑥−4)/ (𝑥2+𝑥−2) 𝑑𝑥 limit from 2 to 3
Correct to 4 significant figures
a) 𝑚 = 𝑛 + 1
𝑑(𝑋𝑚)/𝑑𝑥 = 𝑚𝑋𝑚−1
𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑡𝑖𝑛𝑔 𝑏𝑜𝑡ℎ 𝑠𝑖𝑑𝑒 ∫𝑑(𝑋𝑚)/𝑑𝑥 = ∫𝑚𝑋𝑚−1 𝑑𝑥
∫𝑚𝑋𝑚−1 𝑑𝑥 = 𝑚𝑋𝑚−1+1 /(𝑚−1+1) = 𝑋𝑚 + 𝑘
∫𝑚𝑋𝑛−1 𝑑𝑥= 𝑋𝑚+𝑘
𝑑𝑖𝑣𝑖𝑑𝑒 𝑏𝑜𝑡ℎ 𝑠𝑖𝑑𝑒 𝑏𝑦 𝑚
∫𝑚(𝑋𝑚−1 𝑑𝑥)/ 𝑚 = 𝑋𝑚 /𝑚 + 𝑘/𝑚
∫𝑋𝑛−1 𝑑𝑥 = 𝑋𝑚/𝑚 + 𝑘/𝑚
𝑘/𝑚=𝐶 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 𝑚 = 𝑛+1
Thus; ∫𝑋𝑛−1 𝑑𝑥 = 𝑋𝑛+1 /𝑛+1 + 𝐶
b)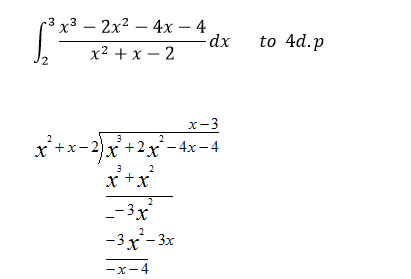
∫ (𝑥 − 3) + (−𝑥 – 4)/(𝑥2 + 𝑥 – 2) dx
∫ (𝑥 − 3) – (𝑥 + 4)/(𝑥2 + 𝑥 – 2) dx
(𝑥 + 4) /(𝑥2 + 𝑥 – 2) = (𝑥 + 4)/ (𝑥 − 1)(𝑥 + 2)
𝑃𝑎𝑟𝑡𝑖𝑎𝑙 𝑓𝑟𝑎𝑐𝑡𝑖𝑜𝑛
𝐴/(𝑥 – 1) + 𝐵/(𝑥 + 2) = 𝑥 + 4/(𝑥 − 1)(𝑥 + 2)
𝐴(𝑥 + 2) + 𝐵(𝑥 − 1) = 𝑥 + 4
𝑊ℎ𝑒𝑛 𝑥 = 1
𝐴(3) = 5 𝐴 =5/3
𝑊ℎ𝑒𝑛 𝑥 = −2
𝐵(−3) = 2 𝐵 = −2/3
Now we have [5/3/(𝑥 – 1)] – 2/3/(𝑥 + 2)]
Inserting this value into the integration we have;
∫ {(𝑥 − 3) − [5/3/(𝑥 – 1)] – [2/3/(𝑥 + 2)]} dx
∫ (𝑥 − 3) − ∫ [5/3/(𝑥 – 1)] – 2/3/(𝑥 + 2)]dx
∫ (𝑥 − 3)dx − ∫ 5/3/(𝑥 – 1)dx + ∫2/3/(𝑥 + 2)dx
∫ (𝑥 − 3)dx − 5/3∫ 1/(𝑥 – 1)dx + 2/3∫1/(𝑥 + 2)dx
[x2/2 – 3x] – [5/3 In(x -1)] + [2/3 In(x+2)]
= −0.5 − 1.1552 + 0.1487 = −1.5064
a) Show directly from definition (i.e from first principle) that derivative of f(x) = 2x3 is 6x2
b) Find the differential coefficient of y = 5x using first principle
a) f(x) = 2x3 is 6x2
Let x be increased by change in x
𝑓(𝑥 + Δ𝑥) = 2(𝑥 + Δ𝑥)3
= 2(𝑥3 + 3𝑥2Δ𝑥 + 3𝑥Δ𝑥2 + Δ𝑥3 )
= 2𝑥3 + 6𝑥2Δ𝑥 + 6𝑥Δ𝑥2 + 2Δ𝑥3
𝑎𝑠 𝑓(𝑥)𝑐ℎ𝑎𝑛𝑔𝑒𝑠 𝑏𝑦 𝑎 𝑟𝑎𝑡𝑒 𝑜𝑓 Δ𝑥
𝑓(𝑥 + Δ𝑥)/Δ𝑥 = (2𝑥3 + 6𝑥2Δ𝑥 + 6𝑥Δ𝑥2 + 2Δ𝑥3 )/Δ𝑥
𝑓(𝑥 + Δ𝑥)/Δ𝑥 = 2𝑥3/Δ𝑥 + 6𝑥2 + 6𝑥Δ𝑥 + 2Δ𝑥
𝑎𝑠 Δ𝑥 → 0
𝑓(𝑥 + Δ𝑥)/Δ𝑥 = 6𝑥2
b) y = 5x
f(x) = y = 5x
𝑓(𝑥+Δ𝑥) = 5(𝑥+Δ𝑥)
𝑓(𝑥+Δ𝑥)=5𝑥+5Δ𝑥
𝑓(𝑥+Δ𝑥)/Δ𝑥=5𝑥/Δ𝑥 + 5
Δ𝑥→0 𝑑𝑦/𝑑𝑥=5
a) Differentiate the following by the general rule
- y= 3(t-2)3
- 𝑦 = 3𝑥 – 1/√𝑥 + 1/𝑥
- 𝑦=6 + 1/𝑥3
b) An alternating Voltage is given by V=100Sin200t Volts, where ‘t’ is the time in seconds. Calculate the rate of change of voltage when
- t=0.005s
- t=0.01s
c) Find the rate of change of ‘y’ with respect to ‘x’ of the following
- y = 3x In2x
- y = 3x2 Sin x
a)
i) y = 3(t-2)2
y = f(x) xn
dy/dx = nXn-1
dy/dt = 2(3)(t-2)2-1
y = 6(t-2)
ii) 𝑦 = 3𝑥 – 1/√𝑥 + 1/𝑥
y = 3x – x-1/2 + x-1
dy/dx = 3 – (-1/2x-1/2-1 + (-1x-1-1)
= 3 + ½ x-3/2 – x-2
𝑑𝑦/𝑑𝑥 = 3 + 1/2𝑥3/2 −1/𝑥2
iii) 𝑦=6 + 1/𝑥3
y = 6 + 1/x3
y = 6 + x-3
dy/dx = 0 -3x-3-1
dy/dx = -3x-4
𝑑𝑦/𝑑𝑥 = −3/𝑥4
b)
V = 100 Sin200t volts
dv/dt = (100)200 Cos 200t
= 200 Cos 200t
i) when t =0.005s
dv/dt = 20000 Cos 200 (0.005)
=20000 Cos 1 = 19996.95 v/s
ii) when t = 0.01s
dv/dt = 2000 Cos 200 (0.10)
= 19987.8 v/s
b)
i) y = 3x In2x
let u=3x and v = In2x
du/dx =3x
v can also be written as v = In2 + Inx
dv/dx = 1/x
dy/dx = udv + vdu
dy/dx = 3x (1/x) + In2x (3x)
dy/dx = 3 + 3x In2x
ii) y = 3x2 Sin x
Let u = 3x2 and v = Sinx
du/dx = 6x dv/dx = Cosx
dy/dx = udv + vdu
dy/dx = 3x2 Cosx + 6x Sinx
a) Differentiate the following using
i) y = 4sin5x/5x2
ii) y = 3√θ3 /2sin2θ
b) Differentiate the following using chain rule
i) y = 3 cos(5x3 + 2)
ii) y = √(3x2 + 4x – 1)
iii) y = (2x3 + 5x)5
i) y = 4sin5x/5x2
Let U = 4sin 5x and v = 5x4
du/dx = 4 × 5 cos5x
dv/dx = 20x3
dy/dx = (Vdu/dx – Udv/dx)/V2
dy/dx = (5x4 × 20cos5x – 4sin5x × 20x3)/(5x4)2
dy/dx = (100x4 cos5x – 80x3sin5x)/25x8
ii)
y = 3√θ3 /2sin2θ = 3θ3/2 /2sin2θ
u = 3θ3/2 and v=2sin2θ
du/dθ =3/2 × 3θ3/2 -1 =9/2θ1/2 =9√θ
dv/dθ = 4cos2θ
Using dy/dθ = (Vdu/dθ – Udv/dθ)/V2
= (2sin2 θ × 9/2 √θ – 3√θ3 × 4cos2θ)/(2sin2θ)2
=(9 √θ sin2 θ – 12√θ3 cos2θ)/(4sin2 2θ)
b)
i) y = (2x3 + 5x)5
let u = 2x3 + 5x and y = u5
dy/dx = dy/du × du/dx
= 5u4 × 6x2 + 5 = 5(6x2 + 5)u4
=(30x2 + 25)u4
=(30x2 + 25)(2x3 + 5x)4
ii) y = √(3x2 + 4x -1)
let u = 3x2 + 4x -1
y = √u = u1/2
dy/dx = dy/du × du/dx
=1/2 u-1/2 × 6x + 4
=1/2(6x +4) × 1/√u
now inserting the value
= 2(3x + 2)/2√(3x2 + 4x – 1)
= (3x + 2)/√(3x2 + 4x – 1)
a)
i) Determine
∫ (11 -3x)/(x2 + 2x -3) dx
ii) Integrate the following indefinite integrals
∫3x4 dx and ∫ 2/x2 dx
b) Evaluate the definite integrals ( where necessary to 4 significant figures)
- ∫41 5x2 dx
- ∫20 3sin t dt
- ∫32 2/3x dx
a)
i) ∫(11 -3x)/(x2 + 2x -3) dx
x2 + 2x – 3 = (x + 3)(x -1)
∫(11 – 3x)/ (x + 3)(x -1) dx
Splitting the equation to partial fraction
A/x+3 + B/x -1 = (11 – 3x)/(x +3)(x – 1)
Multiply through by (x + 3)(x – 1)
A(x – 1) + B(x+3) = 11 -3x
when x = +1
A(0) + B(4) = 8
B = 8/4 = 2
when x = -3
A(-4) = 20
A = -20/4 = -5
Substituting the value of A and B
2/(x+3) + -3/(x -1)
∫2/(x+3) dx – ∫3/(x -1)
2 ∫1/(x+3) – 3∫1/(x-1)
u = x+3 du/dx =1 du=dx
v x+1 dv/dx = 1 dv=dx
2∫1/u du – 3∫1/v dv
2Inu – 3Inv
Inserting the value of U and V
2In(x+3) – 3In(x-1)
b)
i) ∫41 5x2 dx = [5x3 /3] limit from 1 to 4
=5/3[x3] Now inserting the limit;
5/3[43 – 13 ] =105
ii) ∫20 3sint dt = 3[-cos t] limit from 0 to 2
Now inserting the limit;
-3[cos(2) –cos(0) ] =1.827 ×10-3|
Answer to 4 dp is 0.0018
iii)
∫32 2/3x dx = 2/3 ∫32 (1/x) dx
=2/3 [Inx]
inserting the limit 2/3[In3 – In2]
2/3[1.09861 – 0.6931] =0.2703
a) Determine the following
- ∫ 2sin(4x +9)dx
- ∫1/2(5x – 3)6 dx
- ∫10 (3x + 1)5dx
 b) If ∫ 8x3 -3x2 + 4x – 5 dx
b) If ∫ 8x3 -3x2 + 4x – 5 dx
Determine the value of “I” where x = 3, given that at x = 2, I = 26
a)
i) ∫ 2sin(4x +9)dx
Let u = 4x+9
du/dx= 4 dx = du/4
∫ 2sinu du/4 =1/2[-cosu]
= -1/2cos(4x + 9) + C
ii) ∫1/2(5x – 3)6 dx
let u= 5x-3, du/dx = 5 therefore dx= du/5
∫1/2 u6 du/5 =1/10 ∫u6 du
1/10 ×u7 = u7/70
Inserting the value of u (5x-30)/70 + C
iii) ∫10 (3x + 1)5dx
let u= 3x+1, du/dx= 3 therefore dx=du/3
∫10 u5 du/3 = 1/3[u6/6]
Inserting the value of u 1/18 [(3x -1)6]
Putting the limit of 0 to 1
1/18[(3(1) + 1)6 – (3(0) + 1)6 ]
1/18(46 – 16) = 227.5
b) I = ∫8x3 -3x2 +4x -5 dx
=8x4/4 -3x3/3 + 4x2/2 – 5x + C
=2x4 – x + 2x2 -5x +c
When x= 2 and = 26
26 = 2(2)4 – (2)3 + 2(2)2 – 5(2) +C
C+22 = 26
C =4
When x= 3
I = 2(2)4 – (2)3 + 2(2)2 – 5(2) +4 =142
a. Sketch the graph y = x3 + 2x2 – 5x – 6 between x = -3 and x = 2 and determine the area enclosed by the curve and the x – axis.
b. The velocity v of a body t seconds after certain instance is (2t2 + 5 ) m/s. Find by integration how far its moves in the interval from t = 0 to t = 4s and produce a graph.
c. Determine the area enclosed by y = 2x + 3, the x – axis and ordinate x = 1 and x = 4. Produce the graph
a.
y = x3 + 2x2 – 5x – 6 x= -3, x= 2
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -18 | 0 | 4 | 0 | -6 | -8 | 0 | 24 |
Graph of y = x3 + 2x2 – 5x – 6 x= -3, x= 2
∫-1-3 ydx – ∫2-1ydx
∫ydx = ∫ x3 +2x2 -5x -6
=[x4/4 + 2x3/3 – 5x2/2 – 6x]
Inserting the two different limit to the equation -1 to -3 and -1 to 2
Area = 5.33 – ( -15.75) = 21.08
b) Recall v = du/dx and dx =vdt or ∫tt0 vdt
x = ∫40 (2t2 +5)dt = (2t3/3 + 5t)
Inserting the limit we have [2(4)3/3 + 5(4)] – 0 =62.67m
| t | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| v | 7 | 5 | 7 | 13 | 23 | 37 | 55 |
 c. y = 2x + 3 x=1, x=4
c. y = 2x + 3 x=1, x=4
Area =∫41 (2x + 3)dx = [2x3/3 + 3x]
Inserting the limit from 1 to 4
[2(4)3 /3 + 3(4)] – [2(1)3/3 + 3] = 42
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 9 | 11 | 13 |
Differentiate the following
- y = 5x4. Sin x
- y = cos(2x – 3x)
a.
y = x3 + 2x2 – 5x – 6 x= -3, x= 2
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -18 | 0 | 4 | 0 | -6 | -8 | 0 | 24 |
Graph of y = x3 + 2x2 – 5x – 6 x= -3, x= 2
∫-1-3 ydx – ∫2-1ydx
∫ydx = ∫ x3 +2x2 -5x -6
=[x4/4 + 2x3/3 – 5x2/2 – 6x]
Inserting the two different limit to the equation -1 to -3 and -1 to 2
Area = 5.33 – ( -15.75) = 21.08
b) Recall v = du/dx and dx =vdt or ∫tt0 vdt
x = ∫40 (2t2 +5)dt = (2t3/3 + 5t)
Inserting the limit we have [2(4)3/3 + 5(4)] – 0 =62.67m
| t | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| v | 7 | 5 | 7 | 13 | 23 | 37 | 55 |
 c. y = 2x + 3 x=1, x=4
c. y = 2x + 3 x=1, x=4
Area =∫41 (2x + 3)dx = [2x3/3 + 3x]
Inserting the limit from 1 to 4
[2(4)3 /3 + 3(4)] – [2(1)3/3 + 3] = 42
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 9 | 11 | 13 |
Integration can be applied in the calculation of areas, volumes, central points and many more
a) false b) true c) none of the above d) all of the above
True [b]
The differential of y = 3x2 . ex is ?
a) 3xex(x + 3) b) x2ex(x + 3) c) 3x3ex(x + 3) d) 3x2ex(x + 3)
d[(3x2.ex)/dx] = d/dx((3x2).ex) + d(ex). 3x3
9x2ex + 3x3 ex = 3x2 ex (3 + x ) [d]
lim (1 – √x )/(1 -x) by rationalization as x approaches 1 is?
a) 1 b) 1/2 c) 2 d) 0
I = ∫ 4x2 dx = 4x3/3 + C
I = 25 when x = 3 we have 4(3)3/3 + C = 25
(4 x 27)/3 + C = 25 => 36 + C = 25
C = 25 – 36 = – 11 [b]
the integral of ∫ cos x dx is?
a. Sin x b. – Sin x c. – Sin x + C d. Sin x + C
∫ cos x dx = sin x + C [d]
The slope of a constant value (like 1000) is always?
a. 1000 b. 0 c. undefined d. none of the above
slope of constant is always ‘0’ [b]
if f(x) = In(Inx), then (dy/dx) =
a. 1/x b. 1/Inx c. 1/xInx d. Inx/x
derivative of In (In x ) using chain rule, let In x = u such that y = In u => (dy/dx) = 1/x , (du/dx) = 1/x
=> (dy/dx) = (dy/du). (du/dx) = (1/x) x (1/In x) = (1/x Inx) [c]
They equation Xn = nXn-1 is an expression of ?
a. The product rule b. The chain rule c. The power rule d. The substitution rule
(d/dx)[xn] = n xn-1 is an experiment of power rule [c]
What do you understand about calculus?
a. Motion b. speed c. change d. development
calculus is approximately change [c]
what is (u/dx)[(5z2 + z3 – 7z4)]?
a. 10z2 + 3z3 – 14z4 b. 10z + 3z2 – 28z3 c. 10z +3z2 + 28z4 d. 10z +3z – 28z3
d/dx (5z2 + z3 – 7z4) =
10z + 3z2 – 28z3 [b]
∫ 1/x dx =
a. undefined because you cannot divide by zero b. loge(x) c. In(x) d. In(x) + C
∫(1/x) dx = In x + C [d]
which of the following is the best differential technique to use for (x2 + 1)5?
a. the product rule b. The chain rule c. The power rule d. The substitution rule
the best techniques for differential (X2 + 1)5 is a power rule d/dx((g(x))n
= ( n.a.(g1(x)) . (g(x)n-1) [c]
∫10 (x2 – 2x + 1) dx is
a. – 1 b. – 7/3 c. 7/3 d. 1
∫10 ( x2 – 2x + 1 )dx = [ x3/3 – 2x2/2 + x ]10
= [(13/3) – (1)2 + 1 ] – [(03/3) – (0)2 + (0)] = 1/3 – 1 + 1 = 1/3
if y = 3x2 + 2x + 1, then the value od dy/dx at X = 1 is
a. – 2 b. 0 c. 12 d. 8
y = 3x2 + 2x + 1
dy/dx = 6x + 2 , when x = 1 , dy/dx = 6(1) + 2 = 8 [d]
A function might be continuous or not, depends on its?
a. equation b. x – axis c. y- axis d. Domain
. A function might be continuous or not depending on its domain [d]
. Differentiate
- y = 5x2 . sinx
- Y = cos ( 2x – 3x )
- Y = 5x4. Sinx => u = 5x4 v = sin x
(du/dx) 20x3 (dv/dx) = cos x
(dy/dx) = u(dv/dx) + v(du/dx) = 5x4.cos x + 20 x3 sin x ( product rule )
- y = cos ( 2x – 3x ) = cos ( – x )
Let ( – x) = u such that y = cos u
Chain rule: dy/dx = (dy/du) . (du/dx)
du/dx = – 1 , dy/du = – sin u = – sin ( – x )
dy/dx = – 1 x -sin(-x) = sin(-x)
integrates by partial fraction on the given integral
∫ [(3x + 2) / (1 + – 2x3)] dx
[( 5x + 2 )/ ( 1 + x – 2x2] = [ (5x + 2)/(1 – x)(1 + 2x) ] = [ A/(1 – x) ] + [ B/(1 + 2x) ]
multiply through by (1 – x)(1 + 2x)
5x + 2 = A (1 + 2x ) + B (1 – x)
Put (x.1) ; 5(1) + 2 = A (1 + 2(1) + B (1 – 1 )
5 + 2 = 3A
A = 7/3
Put x = (-1/2) ; 5(-1/2) + 2 = A ( 1 + 2(-1/2) + B (1 – (– ½) )
– 5/2 + 2 = 3/2 B
– 1/2 = 3/2 B => B = (– 1/2) x (2/3) = – 1/3
Therefore (5x + 2 )/ ( 1 – x) (1 + 2x2) = [7/3(1 – x )] + ( – 1/ 3(1 + 2x) )
[7/3(1- x)] – [1/3( 1 + 2x )]
∫ (5x + 2 )/ ( 1 + x – 2x2 )dx = -7/3 In(x) – (1/6) In ( 1 + 2x)
= In(x)-7/3 – In (1 + 2x)1/6
= In(x)-7/3/(1 + 2x)1/6)
- use the first principles to find the derivative of f(x) = x3 + 3x
- find dy/dx of 2ex
- evaluate ∫ [(x3 – 25x + 1) / (x3 – 25)]dx
- f(x) = x3 + 3x
From first principle, f1(x) = f(x + dx) – f(x)/dx
f(x + dx ) = ( x + dx )2 + 3(x + dx)
f(x) = x2 + 3x
f1(x) = (x + dx )3 + 3(x + dx) – ( x3 + 3x) / dx
x2 + 2xdx + dx3 + 3x + 3dx = x2 – 3x / dx
2xdx + dx2 + 3dx / dx = dx(2x + dx + 3 ) / dx
f(x) = 2x + dx + 3
lim dx -> 0
f(x) = 2x + (0) + 3 = 2x + 3
- . dy/dx (2ex) = 2. dy/dx (ex)
dex/dx = ex therefore dy/dx (2ex) = 2ex
(x3 – 25x + 1)/ (x2 – 25) =
- [(x3 – 25x + 1)/ (x2 – 25)] . x + 1/x2 – 25
∫ [(x3 – 25x + 1)/ (x2 – 25)] dx = ∫ x dx + ∫ 1/ x2 – 25 dx
∫x dx = x2/2 + C
∫( 1/ x2 – 25 ) dx = ∫ 1/(x – 5 ) (x + 5 ) dx
1/(x – 5)(x + 5) = (A/x-5) + (B/x+5)
1. = A(x + 5) + B(x-5)
For x = 5 1 = A(5 + 5) + B(0) => 10A = 1 => A = 1/10
For x = – 5 1 = A(- 5 + 5) + B(-5 -5) => 1 = – 10B therefore B = – 1/ 10
Therefore ∫ [1/(x – 5)(x + 5)] dx = ∫ [1/10(x + 5)] dx
1/10 In (x – 5 ) = 1 /10 In (x + 5)
In (x – 5)1/10 = In (x + 5)1/10 => In [(x – 5)1/10] / (x + 5)1/10
If you like this video, please click on the Subscribe to our YouTube channel for more standard tutorials
Do you have a Question to Ask?
SmartBukites have a Facebook Group which allows everyone to ask, answer and seek academic help. At SmartBukites, we believe Smart approach to Education will go along way in easing human academic struggle.
Click the link to join now!!! https://web.facebook.com/groups/675122219621351
